The Physical Chemistry of Carbon Dioxide Absorption
Guest post by Hugo Franzen
Perhaps because I have been a Physical Chemist for more years than I care to mention, I have the idea that Physical Chemists have something important to contribute to just about any discussion about physical phenomena. I hope that I can convince you that this is in fact true in the case of global climate change. One reason I feel it important to be a spokesman for Physical Chemistry in this arena is because, for the most part, we P. Chemists feel it important to develop math based arguments that catch the essence of what is occurring. Of course we then leave the hard part of dealing with the ramifications to someone else. What I mean by this in the current discussion is that the problem of global warming can be broken down into two parts – the “forcing” part that deals with the difference between the energy input and output at the earth’s surface and the consequences of that forcing. The latter is the huge problem of the feedbacks and their consequences on the distribution of that energy over the globe.
The second part is the tough, ongoing job of the Climatological community while the first part is basically P. Chem. (even though it was in many cases done by folks in other disciplines). In this essay it is my purpose to discuss the easier, forcing part. When it comes to communication, the considerations in this realm have a distinct advantage in that the results follow directly from the solution of an elementary differential equation using specroscopic data that have been known since the 1960's. I have benefited greatly from others in coming to an understanding of the P. Chem. of Global Warming (GW). I feel myself qualified, on the basis of what I have learned, to say, from the point of view of Physical Chemistry, i.e. rigorous science of the if A then B type, that global warming as the result of carbon dioxide in the atmosphere is totally undeniable and that the extent of the forcing is beyond doubt close to what the climatologists are saying it is. These conclusions are not based on the earth’s temperature history or upon complex computer programs (which I certainly believe to be of great importance – it’s just that they are difficult to communicate about) but upon the type of calculation that is done in P. Chem. courses around the world. The calculation on which this essay is based can be found in the presentation (GWPPT6) linked at the bottom of this post.
Interactions between molecules and electromagnetic radiation have been an important part of Physical Chemistry since its inception. The first scientist to attempt a calculation of the GW (a term he introduced) was Svante Arrhenius, the great Swedish Physical Chemist. He did his climate change work in the mid 1890’s. The understanding of the interactions of molecules with radiation progressed enormously with the advent of Quantum Mechanics, and can easily be called a very mature science at this time. The science involves, among many other things, the observation and interpretation of spectra.
Carbon dioxide is a molecule that has been extensively studied in this way and there is available today an incredible depth of knowledge about the interaction of carbon dioxide with electromagnetic radiation. Among a number of interactions about which a great deal is known there are those involved in taking a carbon dioxide molecule (basically linear oxygen to carbon to oxygen) from its ground bending vibrational state to its first excited bending vibrational state. However in both the initial and the final vibrational states the molecule can be in any one of a very large number of rotational states which are separated by energies very much smaller than the energy difference between the vibrational states. Thus there are many transitions between the various rotational states associated with the ground and first excited vibrational states. Transitions between many pairs of these states can be brought about by absorption of infrared radiation of the correct wave length for each pair, and thus such radiation is absorbed over a range of energies (Fig. 1)
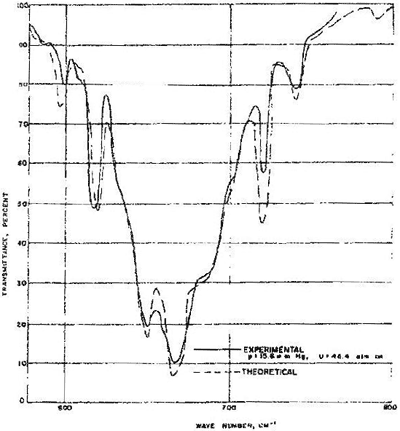These transitions were studied by both theory[i] and experiment[ii] in the 1960’s and the results are highly relevant to global warming, for they provide experimental and calculated data for the linear transmittance of carbon dioxide gas in the infrared region. Transmittance is the fraction of the intensity of a beam that makes it through an absorbing sample. Absorbance is one minus transmittance. Although the data of Fig.1 are for a particular product of path length and carbon dioxide concentration, i.e. a given NL/V, where N/V is the concentration and L is the path length, it should be mentioned that Stull et. al. calculated results for a wide variety of NL/V values and wave lengths. The fit obtained between the calculated and observed spectra for one of the NL/V values (Fig. 1) provides assurance that the absorption coefficients, i.e. the proportionality constants relating the logarithms of the transmittance at the various absorbing wave lengths to the concentration of carbon dioxide in the gas phase, form a reliable basis for calculating the transmittance (or absorbance since they sum to 1) of carbon dioxide in the atmosphere.
The absorption coefficients reported by Stull, et. al. are linear absorption coefficients appropriate to the absorption that results in a decrease in intensity when the radiation is traveling in a single straight line. But the radiation, when the source is the earth, travels in all directions away from the earth. When the radiation is in a single direction, the relevant transmittance is the linear transmittance and the absorption coefficients for linear transmittances were reported by Stull, et. al. The transmittances required when the source is the earth are called the diffuse transmittances and these are calculated by integrating (summing) the intensity equation over all the angles. What results is a diffuse transmittance equation for flux rather than the corresponding equation for decrease in intensity. But this is just what we want to determine the energy audit for the earth, because the flux is the rate at which energy is radiated through a unit area of a surface.
The first task in applying Physical Chemistry to the Global Warming problem is probably to determine the flux of radiation at the earth’s surface. Fortunately in 1900, in his celebrated determination that radiation is quantized, Max Planck solved this problem for equilibrium radiation. It turns out that at equilibrium all matter emits radiation the distribution of which is determined only by its temperature. This distribution, which describes the rate at which energy is emitted at a given wavelength, is given by the Planck equation. But is the earth’s surface at thermal equilibrium? The answer to a very good approximation is yes, provided you restrict your attention to a small enough area and a short enough time. This can be seen immediately when you realize that to say that something is “at thermal equilibrium” means that it has a temperature and vice versa. So the very fact that we can report a temperature for a given place at a given day, and we routinely do that at any place on any day, means that the earth at that time and place is close enough to being in thermal equilibrium that we are justified in talking about its temperature. It then follows that the Planck distribution is a very good approximation to the distribution of the infrared energy radiated by the earth at that place and time.
There remains the problem that the earth then has many different temperatures. In the Earth Sciences it is common practice to use average temperatures as though they were ‘the temperature”. What we believe, and it has been borne out by many studies, is that in general we can do two different things: we can make a number of measurements, reach conclusions based upon those measurements and then average the conclusions, or we can average the measurements and reach conclusions based upon that average measurement. For example we could measure the temperatures at a very large number of places on the earth and 1. Use Planck’s law to calculate the energy radiated at each point and then average or, 2. Average the temperature and use that temperature with Planck’s law to calculate the radiated energy. What has been found is that the final results are essentially the same. In fact temperatures have been measured at a wide range of spots over the earth’s surface and Physicists have looked at the earth’s radiation using satellites. The observed distribution of radiant energy is nicely given by Planck’s Law and the earth’s average temperature. The earth’s spatially averaged temperature, when averaged over a year, comes out to be 288K. The balance: energy in = energy out for the earth for a year results because if the energy in from the sun (corrected for albedo) during a year were greater than the energy radiating out from the earth then the earth’s average temperature would rise and, according to Planck’s Law, the earth would radiate more energy and reestablish the balance. A similar argument holds for antithesis.
So we know the quantity and distribution of the average energy emitted from the earth’s surface from measurement, spectral observation and Planck’s Law. We also know, this time from the data of Stull. et. al. and generalization to the diffuse case, the diffuse transmittances of carbon dioxide for wave length intervals in the energy range of the earth’s Planck radiation. In order to get a “broadband” transmittance, i.e. the transmittance for the energy range over which the carbon dioxide absorbs, the diffuse absorbance for each wave length interval is multiplied by the fraction of the Planck radiation that is emitted in that interval and the product is summed to yield the Planck averaged, broad-band, diffuse transmittances (PABBDT’s) at the various NL/V values for which the linear transmittances were reported by Stull, et. al. These were fit to a curve (PABBDT vs. NL/V) in order to find the dependence of PABBDT for carbon dioxide on NL/V from which we can find the PABBDT of the atmosphere if we know NL/V for the atmosphere.
Thus the one piece of information that is lacking at this point is NL/V of carbon dioxide in the atmosphere. As I am sure everyone reading this essay knows, in 1958, a scientist, Charles David Keeling at the Mauna Loa observatory, initiated a program of measurement of carbon dioxide in the earth’s atmosphere and it has been in operation ever since. The current concentration is somewhere between 385 and 390 ppm. This concentration has been shown to be essentially the same everywhere in the atmosphere. Hence we know, in each case to a very good approximation, the average flux of infrared radiation emitted by the earth as a function of wave length, the PABBDT of carbon dioxide as a function of NL/V and NL/V for the atmosphere.
Therefore we can determine the amount of energy absorbed and reemitted by carbon dioxide in the atmosphere. Because one half of the reemitted radiation comes back to the earth (is the carbon dioxide greenhouse gas flux), this flux is equal to one half the Planck flux in the absorbing interval multiplied by one minus the diffuse, broadband transmittance. Knowing the earth’s average temperature at some initial time and the expected increase in atmospheric carbon dioxide (the Keeling curve) we can calculate the earth’s average temperature difference for these two times as follows. The energy leaving at the final time equals the energy entering at that time (for the reason discussed previously) and, because we know by how much that energy is increased by the carbon dioxide greenhouse effect, we know by how much the earth’s temperature is increased by that effect. When the calculation is done, as in GWPPT6, the conclusion is that the earth’s temperature is currently rising by 0.014 degrees per year because of the greenhouse gas effect of the additional carbon dioxide entering the earth’s atmosphere
In this essay I have restricted myself to words. What I concluded above was accomplished by the solution of equations, and these equations and their solutions are presented in my website. As I see it there are four possibilities 1. Someone could understand the methodology of GWPPT6 on hfranzen.org and agree with the conclusions, or, 2 they might understand and not agree, or, 3 it could be that they do not understand but agree for other reasons,or, 4. they might not understand and not agree. The folks in category 1 need to get the message out. I hope that those in category 2 will contact me with their criticisms. Those in category 3 deserve credit for sound intuitive thinking. Those in the last category are most troublesome. In my view they should either do the hard work of learning the basic science needed for understanding or find someone they trust who understands it to interpret the power point for them. The people of the world need to move on to some very serious changes in our consumption of fossil fuels and there is absolutely no place for obstruction by people who do not understand the nature of the problem.
[i] Stull,Wyatt, and Plass, Applied Optics, V.3,No.2, p.250 (1964)
[ii] Burch, Gryvnak, and Williams, Applied Optics, V.9, p750 (1962)
Posted by hfranzen on Thursday, 23 December, 2010
