When considering the evolution of planetary atmospheres, a critical factor that inevitably comes into the discussion is the gradual brightening of the sun over geological time. Observations that Earth and even Mars likely had liquid water in their distant past, despite a less luminous sun, present a paradox (Sagan and Mullen, 1972): If the sun was so faint, how would the early planets not have been frozen over? Alternatively, if the planets were warm enough to support liquid water then, how are they not extremely hot now? Examining this question is critical to paleoclimate and habitability issues in general, including understanding arguments on why greenhouse gas levels have been higher in the past while still being compatible with relatively cold conditions.
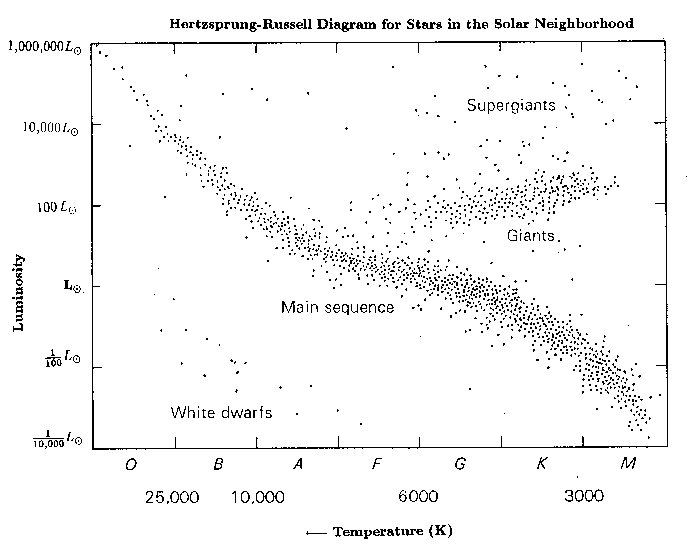
Our own sun is a G2V type star, the ‘V’ also indicating a ‘dwarf,’ or in other words a luminosity classification that tells us the star resides on the “main sequence” (i.e., a locus of points in a plot of stellar luminosity vs. temperature, known to astronomers as a Hertzprung-Russell diagram). It is on the main sequence that the sun will spend most of its lifetime in a stable configuration with nuclear fusion as a power source.

From http://casswww.ucsd.edu/public/tutorial/images/hr_local.gif
Stellar classifications (O, B, A, F, G, K, M), which have become even more finely tuned (for example with numbers, like A0, A1…A9, etc, as the field grows) are characterized according to their spectral properties. Measurements of stellar energy distribution show many narrow wavelength bands with reduced fluxes (i.e., or spectral lines) due to absorption by atoms and ions in the surface layer of the star. The strength of lines and the elemental abundances are in turn affected by temperature. Hydrogen has the strongest lines for A, B, and F stars, while for ‘redder’ stars hydrogen lines are weaker, and heavy atoms may be seen. M-dwarfs are low mass stars (between ~0.08-0.5 Msun) with temperature of about 2,400-3,900 K (compared to 5,800 K for our sun) and luminosities of 0.02-6% of our own sun. Giants and White dwarfs are distinguished from main-sequence stars above. Note that luminosity is a measure of the total power output (for example in Watts), so a star can still have a high luminosity even with a relatively low temperature if it is very big. Likewise, white dwarfs are very hot, but are rather small and so have a weak luminosity.
In this post, we are interested in the question of why the sun actually evolves in the way it does. The implications for planetary atmospheres will be discussed in a follow up Part 2.
We cannot directly observe the evolution of a single star, since they evolve on timescales far longer than humans observe them, although how the luminosity can increase with time on the main-sequence is generally well-accepted. This is through sound theoretical models, but also because we can observe clusters of stars elsewhere in the galaxy with hundreds of thousands of stars (and different masses) in order to build confidence in stellar evolution theory.
The key to understanding the evolution of stellar atmospheres relates directly to the principle of hydrostatic balance, the same fundamental force balance which allows Earth’s atmosphere to stand up as it does (rather than gravity collapsing all the air molecules into a thin layer near the surface). In a hydrostatically balanced atmosphere, the downward force due to gravity is also compensated for by a force upward that results from the pressure of the underlying fluid. In other words, hydrostatic equilibrium defines a balance between gravity and the vertical pressure gradient. If the constraints imposed by hydrostatic balance were not obeyed to high accuracy, than even for a body as large as the sun, noticeable fluctuations in its radius would occur over a characteristic dynamical timescale of just many minutes to an hour.
The next step toward understanding stellar evolution is nuclear fusion, which occurs in the solar core. It turns out that the easiest nuclear reaction is one between a proton and a deuteron. The timescale for two protons to form a deuteron however is rather slow, on the order of 1010 years, but this slow rate helps to set the timescale over which the sun evolves on the main-sequence. Once deuterium is formed, it can smash into another proton to make Helium-3, which can in turn react with He3 again, or for temperatures higher than about 1.4×107 K (achievable in the stellar interior), He3 prefers to react with He4 (various possible paths are shown here ). In any case, what we’ve ended up doing is converted 4 hydrogen atoms into a Helium nucleus. The decrease in hydrogen abundance as it is converted to Helium is critical to the sun’s evolution. The important point for evolution on the main sequence is that this process leads to an increase in the mean molecular weight in regions where fusion is important. At still higher temperatures, other fusion chains like the CNO cycle or the triple-alpha process become important. The ideal gas law gives a relation:

where P is the pressure at the center of the star, R is a constant, ρ is the density of the gas, μ is the mean molecular weight, and T is the temperature. As μ changes, the temperature and pressure must also change to compensate, which in turns impacts the stellar luminosity. How does this work?
Stars become helium rich over time only in the interior, while hydrogen remains abundant in the outer envelope, since the core is where nuclear fusion is most efficient. In the core, there is a consequent reduction over time in the number of particles per unit mass. From the ideal gas law, the decreased pressure of this sphere is no longer sufficient to support the overlying envelope, so if you were to imagine a hypothetical sphere drawn out in the sun, the increase in helium makes it impossible for the sphere to stay at the same radius. Contraction occurs and as the core density goes up, gravitational potential energy is released and (through something called the virial theorem) half of energy is radiated away and half increases temperature of the gas . The luminosity also increases, which is reflected in an increase in the solar irradiance striking a planet. Gough (1981) proposed the following general equation to describe the luminosity as a function of time:

where L(t0) is the luminosity at the current age of the sun, t0 ≈4.6 billion years, and L(t) is the luminosity at time t. It follows for example that 3.5 billion years ago, the solar luminosity was at only ~76% of today's value, while during the Neoproterozoic ~700 mya near the last snowball episode, it was ~94% of today's value.
Since there is still hydrogen in the core of the sun, slow evolution on the main sequence will occur for a few billion years still. The central contraction will cause a hydrogen “shell” to get hotter and burn more strongly (note that eventually the CNO-cycle dominates, and energy generation becomes concentrated in a narrow region around a helium-rich core), and high interior temperatures and pressures are too high to be in equilibrium with gravitational forces. The extra energy output results in the dramatic envelope expansion that causes the sun to evolve onto the red giant phase. This terminates the main-sequence phase of the star’s life, and by this time the surface of the sun will actually be somewhat cooler, but its radius will be extremely large (engulfing Mercury for example) and overall luminosity much higher. Considerable mass loss can occur on the Red Giant Branch, in which case Venus and Earth's orbit will be moved outward (inversely related to the mass), potentially being saved from being completely engulfed.
The duration over which other stars will evolve on the main-sequence, as well as the rate at which end phases of its evolution cause it to expand, contract, or change its surface gravity depend largely on its mass. The evolution of stars will therefore differ depending on initial characteristics; for high mass stars for example, the details outlined above are modified somewhat in that they have a convective core, so the newly formed helium actually becomes well-mixed in the stellar interior.
When considering stellar evolution and the prospect of life evolving, it is worth noting that the lifetime on the main sequence is inversely related to the mass, to a power generally between 3-4, a consequence of the efficiency at which they burn fuel. This means large O-type stars may only last a couple million years on the main-sequence, while no one will ever find remnants of former main-sequence M-types, since their lifetime is longer than the current age of the universe. M-types therefore are more stable than stars like our own with respect to luminosity variations.
Posted by Chris Colose on Wednesday, 23 March, 2011
 |
The Skeptical Science website by Skeptical Science is licensed under a Creative Commons Attribution 3.0 Unported License. |