Climate Science Glossary

Term Lookup

Enter a term in the search box to find its definition.

Settings

Use the controls in the far right panel to increase or decrease the number of terms automatically displayed (or to completely turn that feature off).

Term Lookup

Term:

Settings

Beginner Intermediate Advanced No Definitions Definition Life:

All IPCC definitions taken from Climate Change 2007: The Physical Science Basis. Working Group I Contribution to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, Annex I, Glossary, pp. 941-954. Cambridge University Press.

Home

Arguments

Software

Resources Comments

The Consensus Project

Translations

About Support

	Climate's changed before
	It's the sun
	It's not bad
	There is no consensus
	It's cooling
	Models are unreliable
	Temp record is unreliable
	Animals and plants can adapt
	It hasn't warmed since 1998
	Antarctica is gaining ice
	View All Arguments...

Latest Posts

Archived Rebuttal

This is the archived Advanced rebuttal to the climate myth "Venus doesn't have a runaway greenhouse effect". Click here to view the latest rebuttal.

What the science says...

Venus very likely underwent a runaway or ‘moist’ greenhouse phase earlier in its history, and today is kept hot by a dense CO₂ atmosphere.

In keeping with my recent theme of discussing planetary climate, I am revisiting a claim last year made by Steven Goddard at WUWT (here and here, and echoed by him again recently) that “the [runaway greenhouse] theory is beyond absurd,” and that it is pressure, not the greenhouse effect that keeps Venus hot. My focus in this post is not on his alternative theory (discussed here), but to discuss Venus and the runaway greenhouse in general, as a matter of interest and as an educational opportunity. In keeping my skepticism fair, I’d also like to address claims (sometimes thrown out by Jim Hansen in passing by) that burning all the coal, tars, and oil could conceivably initiate a runaway on Earth.

It is worth noting that the term runaway greenhouse refers to a specific process when discussed by planetary scientists, and simply having a very hot, high-CO₂ atmosphere is not it. It is best thought of as a process that may have happened in Venus’ past (or a large number of exo-planets being discovered close enough to their host star) rather than a circumstance it is currently in.

A Tutorial of Present-Day Venus

Venus’ orbit is approximately 70% closer to the sun, which means it receives about 1/0.7² ~ 2 times more solar insolation at the top of the atmosphere than Earth. Venus also has a very high albedo which ends up over-compensating for the distance to the sun, so the absorbed solar energy by Venus is less than that for Earth. The high albedo can be attributed to a host of gaseous sulfur species, along with what water there is, which provide fodder for several globally encircling sulfuric acid (H₂SO₄) cloud decks. SO₂ and H₂O are the gaseous precursor of the clouds particles; the lower clouds are formed by condensation of H₂SO₄ vapor, with SO₂created by photochemistry in the upper clouds. Venus’ atmosphere also has a pressure of ~92 bars, nearly equivalent to what you’d feel swimming under a kilometer of ocean. The dense atmosphere could keep the albedo well above Earth’s even without clouds due to the high Rayleigh scattering (the effect of clouds on Venus and how they could change in time is discussed in Bullock and Grinspoon, 2001). Less than 10% of the incident solar radiation reaches the surface.

Observations of the vapor content in the Venusian atmosphere show an extremely high heavy to light isotopic ratio (D/H) and is best interpreted as a preferential light hydrogen escape to space, while deuterium escapes less rapidly. A lower limit of at least 100 times its current water content in the past can be inferred (e.g. Selsis et al. 2007 and references therein).

The greenhouse effect on Venus is primarily caused by CO₂, although water vapor and SO₂ are extremely important as well. This makes Venus very opaque throughout the spectrum (figure 1a), and since most of the radiation that makes its way out to space comes from only the very topmost parts of the atmosphere, it can look as cold as Mars from IR imagery. In reality, Venus is even hotter than the dayside of Mercury, at an uncomfortable 735 K (or ~860 F). Like Earth, Venusian clouds also generate a greenhouse effect, although they are not as good infrared absorbers/emitters as water clouds. However, the concentrated sulfuric acid droplets can scatter infrared back to the surface, generating an alternative form of the greenhouse effect that way. In the dense Venusian CO₂ atmosphere, pressure broadening from collisions and the presence of a large number of absorption features unimportant on modern Earth can come into play (figure 1b), which means quick and dirty attempts by Goddard to extrapolate the logarithmic dependence between CO₂ and radiative forcing make little sense. The typical Myhre et al (1998) equation which suggests every doubling of CO₂ reduces the outgoing flux at the tropopause by ~4 W/m², although even for CO₂ concentration typical of post-snowball Earth states this can be substantially enhanced. Figure 1b also shows that CO₂ is not saturated, as some skeptics have claimed.

_{Figure 1: a) Radiant spectra for the terrestrial planets. Courtesy of David Grisp (Jet Propulsion Laboratory/CIT), from lecture "Understanding the Remote-Sensing Signatures of Life in Disk-averaged Planetary Spectra: 2" b) Absorption properties for CO2. The horizontal lines represent the absorption coefficient above which the atmosphere is strongly absorbing. The green (orange) rectangle shows that portion of the spectrum where the atmosphere is optically thick for 300 (1200) ppm. From Pierrehumbert (2011)}

How to get a Runaway?

To get a true runaway greenhouse, you need a conspiracy of solar radiation and the availability of some greenhouse gas in equilibrium with a surface reservoir (whose concentration increases with temperature by the Clausius-Clapeyron relation). For Earth, or Venus in a runaway greenhouse phase, the condensable substance of interest is water— although one can generalize to other atmospheric agents as well.

The familiar water vapor feedback can be illustrated in Figure 2, whereby an increase in surface temperature increases the water vapor content, which in turn results in increased atmospheric opacity and greenhouse effect. In a plot of outgoing radiation vs. temperature, this would result in less sensitive change in outgoing flux for a given temperature change (i.e., the outgoing radiation is more linear than one would expect from the σT⁴ blackbody-relation).

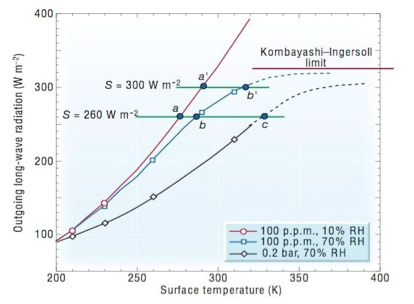
_{Figure 2: Graph of the OLR vs. T for different values of the CO2 content and relative humidity. For a fixed RH, the specific humidity increases with temperature. The horizontal lines are the absorbed shortwave radiation, which can be increased from 260-300 W m^-2. The water vapor feedback manifests itself as the temperature difference between b’-b and a’-a, since water vapor feedback linearizes the OLR curve. Eventually the OLR asymptotes at the Komabayashi-Ingersoll limit. Adopted from Pierrehumbert (2002)}

One can imagine an extreme case in which the water vapor feedback becomes sufficiently effective, so that eventually the outgoing radiation is decoupled from surface temperature, and asymptotes into a horizontal line (sometimes called the “Komabayashi-Ingersoll” limit following the work of the authors in the 1960’s, although Nakajima et al (1992) expanded upon this limiting OLR in terms of tropospheric and stratospheric limitations). In order to sustain the runaway, one requires a sufficient supply of absorbed solar radiation, as this prevents the system from reaching radiative equilibrium. Once the absorbed radiation exceeds the limiting outgoing radiation, then a runaway greenhouse ensues and the radiation to space does not increase until the oceans are depleted, or perhaps the planet begins to get hot enough to radiate in near visible wavelengths.

_{Figure 3: Qualitative schematic of how the ocean reservoir is depleted in a runaway. From Ch. 4 of R.T. Pierrehumbert’s Principles of Planetary Climate}

On present-day Earth, a “cold trap” limits significant amounts of water vapor from reaching the high atmosphere, so its fate is ultimately to condense and precipitate out. In a runaway scenario, this “cold trap” is broken and the atmosphere is moist even into the stratosphere. This allows energetic UV radiation to break up H₂O and allow for significant hydrogen loss to space, which explains the loss of water over time on Venus. An intermediate case is the “moist greenhouse” (Kasting 1988) in which liquid water can remain on the surface, but the stratosphere is still wet so one can lose large quantities of water that way (note Venus may never actually encountered a true runaway, there is still debate over this). Kasting (1988) explored the nature of the runaway /moist greenhouse, and later in 1993 applied this to understanding habitable zones around main-sequence stars. He found that a planet with a vapor atmosphere can lose no more than ~310 W/m², which corresponds to 140% of the modern solar constant (note the albedo of a dense H₂O atmosphere is higher than the modern), or about 110% of the modern value for the moist greenhouse.

Earth and the Runaway: Past and Future

Because Earth is well under the absorbed solar radiation threshold for a runaway, water is in a regime where it condenses rather than accumulating indefinitely in the atmosphere. The opposite is true for CO₂, which builds up indefinitely unless checked by silicate weathering or ocean/biosphere removal processes. In fact, a generalization to the runaway threshold thinking is when the solar radiation is so low, so that CO₂ condenses out rather than building up in the atmosphere, as would be the case for very cold Mars-like planets. Note the traditional runaway greenhouse threshold is largely independent of CO₂ (figure 2 & 4; also see Kasting 1988), since the IR opacity is swamped by the water vapor effect. This makes it very difficult to justify concerns over an anthropogenic-induced runaway.

_{Figure 4: The H2O–CO2 greenhouse. The plot shows the surface temperature as a function of radiated heat for different amounts of atmospheric CO2 (after Abe 1993). The albedo is the fraction of sunlight that is not absorbed (the appropriate albedo to use is the Bond albedo, which refers to all sunlight visible and invisible). Modern Earth has an albedo of 30%. Net insolations for Earth and Venus ca. 4.5 Ga (after the Sun reached the main sequence) are shown at 30% and 40% albedo. Earth entered the runaway greenhouse state only ephemerally after big impacts that generated big pulses of geothermal heat. For example, after the Moon-forming impact the atmosphere would have been in a runaway greenhouse state for ∼2 million years, during which the heat flow would have made up the difference between net insolation and the runaway greenhouse limit. A plausible trajectory takes Earth from ∼100 bars of CO2 and 40% albedo down to 0.1–1 bar and 30% albedo, at which point the oceans ice over and albedo jumps. Note that CO2 does not by itself cause a runaway. Also note that Venus would enter the runaway state when its albedo dropped below 35%. Se e Zahnle et al 2007}

This immunity to a runaway will not be the case in the long-term. In about a billion years, the sun will brighten enough to push us into a state where hydrogen is lost much more rapidly, and a true runaway greenhouse occurs in several billion years from now, with the large caveat that clouds could increase the albedo and delay this process.

Interesting, some (e.g.. Zahnle et al 2007) have argued that Earth may have been in a transient runaway greenhouse phase within the first few million years, with geothermal heat and the heat flow from the moon-forming impact making up for the difference between the net solar insolation and the runaway greenhouse threshold, although this would last for only a brief period of time. Because the runaway threshold also represents a maximum heat loss term, it means the planet would take many millions of years to cool off following such magma ocean & steam atmosphere events of the early Hadean, much slower than a no-atmosphere case (figure 5).

_{Figure 5: Radiative cooling rates from a steam atmosphere over a magma ocean. The radiated heat is equal to the sum of absorbed sunlight (net insolation) and geothermal heat flow. The plot shows the surface temperature as a function of radiated heat for different amounts of atmospheric H2O (adapted from Abe et al. 2000). The radiated heat is the sum of absorbed sunlight (net insolation) and geothermal heat flow. The different curves are labeled by the amount of H2O in the atmosphere (in bars). The runaway greenhouse threshold is indicated. This is the maximum rate that a steam atmosphere can radiate if condensed water is present. If at least 30 bars of water are present (a tenth of an ocean), the runaway greenhouse threshold applies even over a magma ocean. Note that the radiative cooling rate is always much smaller than the σT⁴ of a planet without an atmosphere}

Conclusions

Venus likely underwent a runaway or “moist greenhouse” phase associated with rapid water loss and very high temperatures. Once water is gone, silicate weathering reactions that draw down CO₂ from the atmosphere are insignificant, and CO₂ can then build up to very high values. Today, a dense CO₂ atmosphere keeps Venus extremely hot.

Updated on 2011-04-11 by Chris Colose.

The Consensus Project Website

THE ESCALATOR

(free to republish)

Home | Translations | About Us | Privacy | Contact Us