Greenhouse Effect Basics: Warm Earth, Cold Atmosphere
Posted on 29 February 2012 by Tom Curtis
Heating and Heat Flow
Some physics, everyone knows. In our daily lives we encounter the effects of physics all the time, and as a result, we know what physics predicts in those circumstances at a gut level. We may not be able to put it into numbers. We may not be able to apply it in novel situations. But we know it all the same.
One example is as simple as putting on a blanket. We know that if we want warm something up, we can increase the supply of heat - or we can reduce the escape of heat. Either is effective. If you have a pot that is simmering and you want to bring it to the boil, you can turn the heat up, or you can put on the lid. If we put on the lid, the pot will go nicely from simmering to boiling, and we don't need to turn up the heat even slightly. Indeed, if we are not careful to turn down the heat, the pot may well boil over.
Likewise, if you have two identical motors running with an identical load and speed (Revolutions Per Minute), one with the water pump working and one without, we are all physicist enough to say that the second one will run hotter. It does not matter that the energy supplied as fuel is identical in both cases. The fact that heat escapes more easilly with water circulating through the radiator will keep the first cooler. The consequence is that stopping the the water from circulating will lead second motor to disaster.
Nor do we find people who doubt this. Suppose somebody told us their water pump was broken, but that the Second Law of Thermodynamics prohibited transfer of heat from a cooler place (the water) to a hotter place (the engine block), so they'ld be fine so long as they didn't rev any faster than normal, we'ld look at them in complete disbelief. Or we would if we were too polite to burst out laughing. And if they set out cross country confident in their belief, it doesn't matter what destination they claim they're heading for. Rather, as we all know, they're really heading for a breakdown!

(Image copyright to iStock, and not to be reproduced without their permission.)
Heat Flow to Space
This physics that everyone knows is not only true of pots and radiators. It is true of the Earth as well. The Earth is warmed by our remarkably stable Sun. As a result, the Earth's surface radiates energy to space, and over time the incoming energy balances the outgoing energy. The process is made more complicated, however, by the existence of Infra Red (IR) absorbing molecules in the atmosphere.
Without those molecules, Infra Red radiation from the Earth's surface would travel directly to space, cooling the Earth quickly and efficiently. At certain wavelengths of Infra Red radiation, however, those molecules absorb many, or all, of the photons emitted from the Earth's surface. That energy is often redistributed among other molecules by collision, but eventually some of the redistributed energy will be reradiated by the Infra Red absorbing molecules. This process absorption, redistribution and then re-emission may occur many times before the energy escapes the atmosphere, but eventually it will either by being emitted to space, or back to the surface.
Intuitively, the energy that goes through multiple stages of absorption, redistribution and re-emission will not escape to space as fast that which is emitted directly to space from the surface. This intuition is sound, but it depends essentially on one factor, the temperature of the atmosphere.
We can see this by considering a fundamental law that governs the radiation of energy, the Stefan-Boltzmann Law:
![]()
In words, that is J-star equals epsilon sigma T to the fourth power, but we don't need to worry about that. What we need to notice is that J-star, which is the energy radiated over a given time from a given area, is proportional to the fourth power of T, ie, temperature. If the temperature doubles, the energy radiated increases sixteen-fold. If it triples, it increases eighty-one- fold. And so on. So, if the temperature of the atmosphere is different from that of the surface, the absorption, redistribution and re-emission of IR radiation by molecules in the atmosphere will certainly change the rate at which heat escapes to space.
Higher is Colder
There is another piece of physics everyone knows. It is that as you go higher in the atmosphere, the atmosphere gets colder. That is the reason why some mountain peaks are snow covered while their bases are still warm. This is not a universal law. It is not true, for example, in the stratosphere where the absorption of UltraViolet radiation from the Sun causes temperatures to rise with increased height. But eighty percent of the Earth's atmosphere is in the troposphere (the lowest layer of the Earth's atmosphere), and most radiation leaving the top of the troposphere escapes to space. And in the troposphere, as you get higher, the temperature gets lower. On average, the temperature drops by 6.5 degrees C for every thousand meters of altitude you climb. That means, for example, that the temperatures fall by about 24.5 degrees C as you climb to the summit of Mount Fuji, and by 50 to 100 degrees as you rise to the top of the troposphere.

We have already seen that temperature significantly effects the radiation of heat. Colder objects radiate less energy, and the Infra-Red absorbing molecules in the atmosphere are colder than the surface. Therefore it is no surprise that the Infra-Red absorbing molecules in the atmosphere radiate less energy to space than they absorb from the warmer surface. That difference is the essence of the greenhouse effect.
No More Arm Waving
It would be helpfull to recapitulate at this point. So far we have noted four simple facts:
- That if you reduce the escape of heat, but do not reduce the incoming heat, things warm up;
- That the atmosphere contains molecules that absorb Infra-Red radiation;
- That radiated energy depends on the temperature of the radiating object; and
- That the atmosphere gets cooler as you get higher, so that the Infra-Red absorbing molecules in the atmosphere radiate less energy to space than they absorb from the surface.
These four facts imply the existence of an atmospheric greenhouse effect, ie, that the presence of Infra-Red absorbing molecules in the atmosphere results in the surface being warmer than it otherwise would be.
In science, however, purely verbal reasoning like this is considered suspect. The reason is that sometimes odd effects occur that render verbal reasoning moot. So in science, there is no substitute for putting the theory into a mathematical form. It gets rid of the arm waving.
Fortunately for us, scientists have already put this theory into mathematical form, at a very detailed level. We can access this work, free of charge, by using the Modtran Model. The Modtran Model shows the radiation up or down over a column of atmosphere under particular conditions. By changing the conditions, you can explore the predicted effects of those changes on upward or downward radiation at any level of the atmosphere from 0 to 70 kilometers altitude. Setting the altitude to 70 kilometers effectively shows the radiation upward to space from the top of the atmosphere, or downward from space at the top of the atmosphere. Setting the altituded to 0 kilometers effectively shows the radiation upward, or downward at the surface.
Using Modtran, I determined the energy output looking downwards from an altitutude of 70 kilometers using the US Standard Atmosphere (1). The result can be seen on the following graph as the green shaded area. I repeated the model run, but this time with the altitude set at 0 km. The result is shown by the outer curve defining the red area in the graph below. That means that the red area itself, which is the upwards radiation from the surface minus the upward radiation to space, is the reduction in energy radiated to space because of the presence of Infra-Red absorbing molecules in the atmosphere. That is, it is the greenhouse effect.
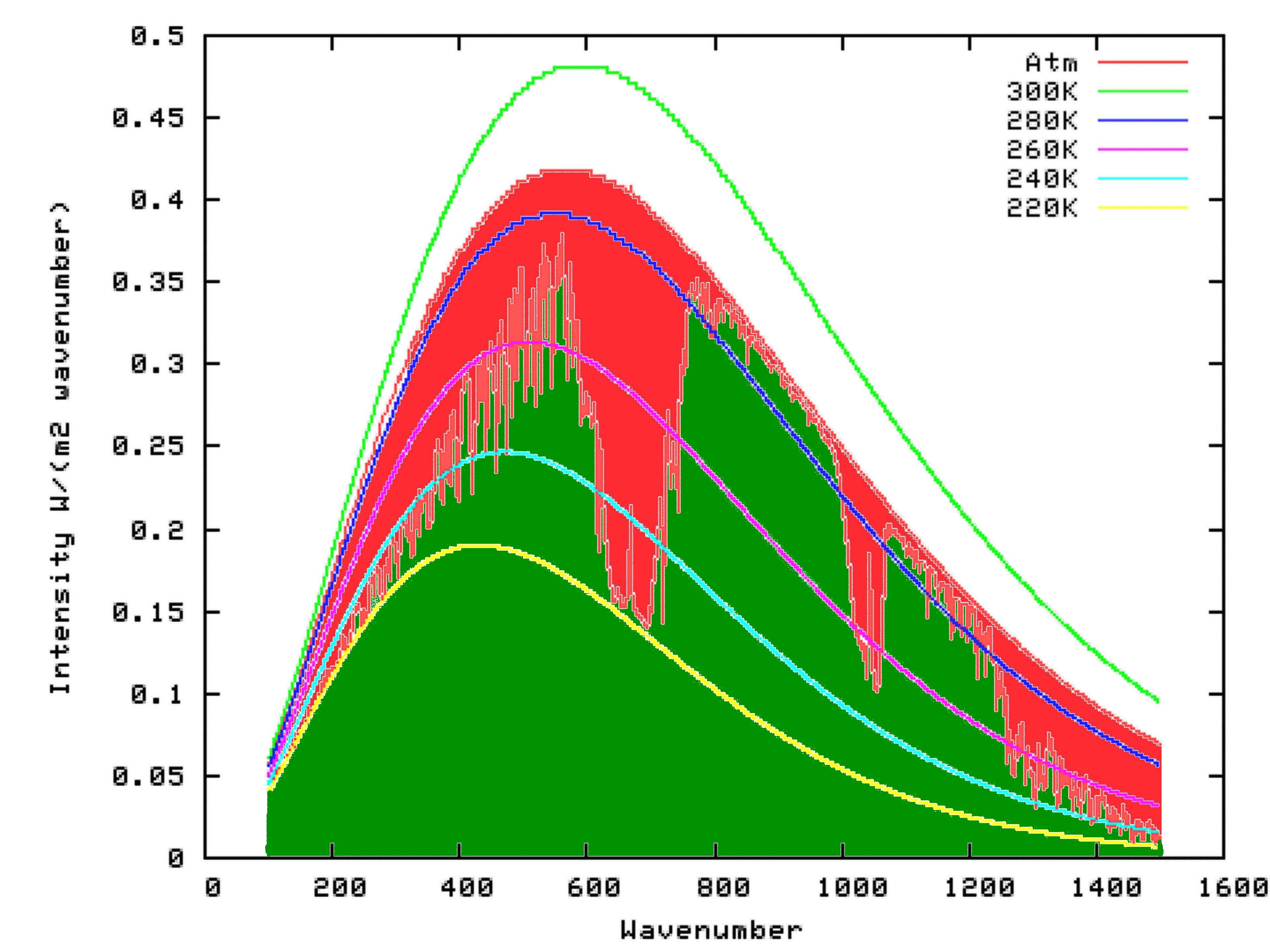
Settled Science
We have all heard how inaccurate models can be. Therefore the fact that a particular model predicts this difference in radiation only shows what the theory predicts. It does not show what is actually happening.
Scientists are not happy with theories whose only support is a model. So in 1969, Conrath and associates compared the results of model calculations of radiation to space with the actually observed radiation using the IRIS instrument on the Nimbus 3 Satellite. The following graph shows the result of their comparison. The dotted line shows the modelled values, while the solid line shows the observed values:
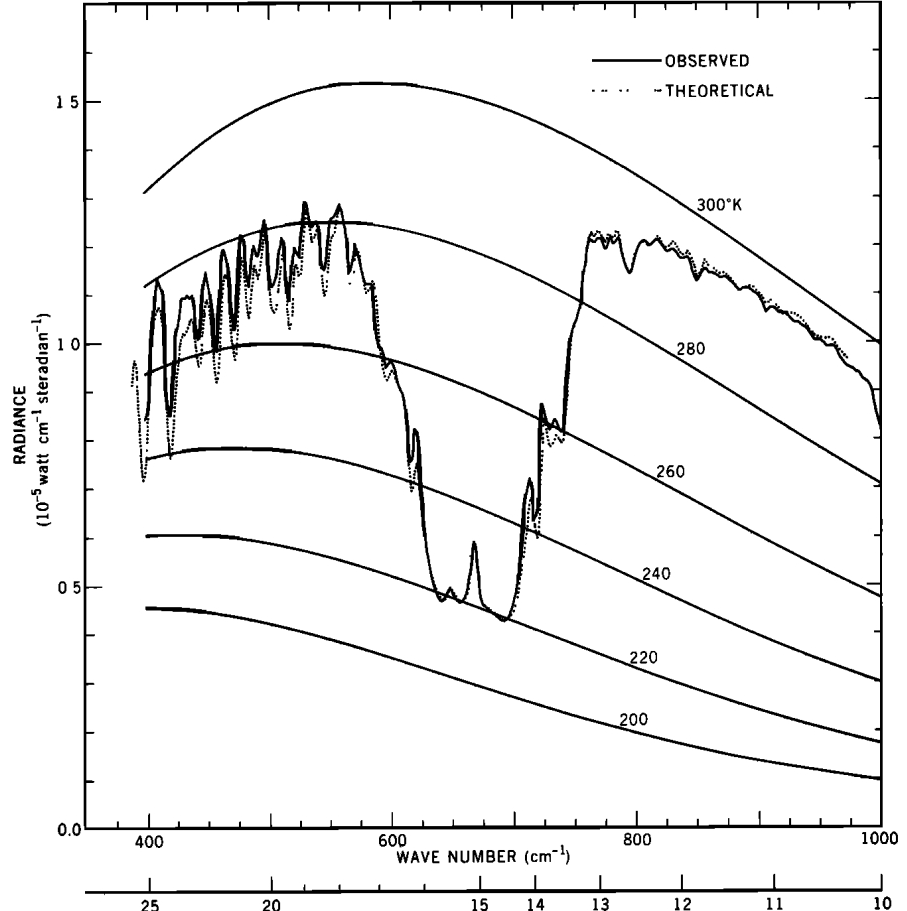
The effect of a particular Infra-Red absorbing molecule, Carbon Dioxide, is clearly visible. With the publication of this data in 1970, the greenhouse effect ceased to be theoretical. It was an observed fact.
Footnote:
(1) Default settings except for adjusting surface temperatures (Ground T offset, c) to approximately match the Earths Global Mean Surface Temperature (about -10 degrees C offset).































 Arguments
Arguments






























Phil, regarding comment 100:
Thanks for suggesting another course of reading and discussion. I looked over the article and a few of the comments in the myth: Is the CO2 effect saturated? as you suggested. That article is listed as "intermediate." I’m still working on the basics, and would like to continue to develop my understanding in the current discussion: Greenhouse Effect Basics: Warm Earth, Cold Atmosphere. In school they taught us to break down complex ideas into components, and then assemble the big picture. Once I have a good visualization of the interaction of the earth’s blackbody radiation and the greenhouse effect, I plan to work my way up to the other source of photons in the wavelength range that is related to v2 CO2 pumping.
So far, it seems to me that the earth’s blackbody radiation in the range 13-18 microns (770 to 560 cm-1) is indeed trapped by CO2 and doesn't get radiated to space, but does in fact cause warming by the v2 CO2*->CO2 transition through collisions with atmospheric gases. If I don’t quite have it right yet, then hopefully someone will help me improve my understanding.
MThompson - Quite right, complete absorption at peak CO2 frequencies occurs with 10's of meters at sea level.
Those 10's of meters of gas then isotropically emit in the same spectra, a portion of which goes upwards to the next higher layer of gas, and so on, and so on, with the sum emission at each layer determined by atmospheric temperature. The effective emission altitude for CO2 is where the air (and GHGs) are thin enough that ~50% of the radiation emitted upwards makes it to space without absorption. And according to the atmospheric lapse rate, that is a cooler layer of air, emitting less radiation than warmer surface air.
The overall effect of the many emission/absorption events and the lapse rate is that there is less radiation from effective emission altitudes than from the surface, a lower effective emissivity of the Earth to space in IR, and hence a higher Earth surface temperature required (by the Stefan-Boltzmann relationship) to emit the energy from incoming sunlight than there would be without the greenhouse gasses - that higher temperature being the greenhouse effect in action.
Regarding 89 and 96:
I need to make a correction for my calculation of the population of the first excited vibrational state for the bending mode of CO2. The ground state wave function is indeed non-degenerate and the first excited state is doubly degenerate, so there is a degeneracy factor of 2 for the Boltzmann distribution calculation. At 25C (77 F) the equilibrium percent of CO2 in the first excited state is 7.4%.
I was a 'climate skeptic' because until reading this page I have never come across a satisfactory explanation of exactly how the GHE works. Well done and thanks to everyone who has contributed to this page. One thing I have always found helpful in understanding things is considering limits so maybe someone can answer these two questions. How would temperatures at ground level change if all CO2 was removed from the atmosphere? How would temperatures at ground level change if all the atmosphere was 100% CO2 and the average air pressure at sea level the same as now? I'm also curious as to what height is 50% of the ground IR radiation converted to heat in the atmosphere.
unspecial, I suspect you'll be getting a detailed answer shortly, but in the meantime, Lacis et al. 2013 provides a few of the answers.
unspecial @101, first thankyou. It is nice to know the effort involved is appreciated.
Turning to your questions:
1) With the removal of all CO2 temperatures would plumet. Of necessity, we can only determine by how much using models, and the best attempt to run this experiment that I am aware of is in Lacis et al (2010). They show global temperatures falling to -21 C with the removal of all CO2, a reduction of 35 C from the current average. By latitude, the reduction of temperatures looks like this:
You will notice that temperatures above freezing are only found in a small band north of the equator. That means that essentially the entire ocean is frozen. However, Lacis et al (2010) is not a complete answer in that their model did not allow the growth of ice sheets and glaciers. The further loss of albedo from that growth would in fact reduce global temperatures further still.
2) It is more difficult to say how temperatures would change with a 100% CO2 atmosphere as I am unaware of any attempts to model that situation. Using the modtran model (used to produce the third image in the OP), we can show that the initial reduction in outgoing radiation looks like this:
The initial reduction in upward IR radiation at the top of the atmosphere is very large (approximately 50 W/m^2), but not as severe as that on Venus due to the lower atmospheric pressure and altitude. There will be a further initial reduction not shown in the modtran model because a pure CO2 atmosphere would have a higher lapse rate.
Taking the 50 W/m^2 and a Equilibrium Climate Sensitivity of 3 C per doubling, that would yield a mean global surface temperature of 13.5 C above current values, or around 28 C. The figure is very approximate because climate sensitivity increases with increasing temperatures over a small increase due to the fact that water vapour concentration will increase with the fourth power (square of the square of) the increase in temperature. The real increase may be between half to double that (ie, 21 to 42 C GMST). Because increased greenhouse effect reduces the temperature difference between poles and equator, the net effect would be tropical or greater temperatures across the entire globe.
It should be noted that we would not get a runaway greenhouse effect as occurred on Venus. That is because the sunlight is too weak at this distance from the Sun to initiate the process. (A more technical explanation is given here.)
3) The altitude at which 50% of the IR from the ground is absorbed will depend on water vapour content in the atmosphere, and cloud height, and so will vary from place to place. Typically it will occur within a kilometer of the surface. Of course, the upward IR radiation from the ground in the frequencies in which it is absorbed will be replaced by an almost equal amount of upward IR radiation from the lower atmosphere, which is very close in temperature to the ground.
Thank you Tom for your answers. It's amazing how finely tuned this planet is in so many ways to support life here. As well as a lapse rate of 6.5 degrees per Km going up we have a lapse rate of 25 degrees going down. E:\Users\Steve\Documents\Science\Geothermal gradient - Wikipedia, the free encyclopedia.htm
1) I had absolutely no idea that CO2 warmed us by 35 degrees. I imagine it affects the daily temp range as well.
2) My question about a 100% CO2 atmosphere is hypothetical but in hindsight is a bit silly as water will always be a part of the equation. Do clouds rise as they get older because they absorb radiation which makes them rise via convection?
3) > The altitude at which 50% of the IR from the ground is absorbed will depend on water vapour content in the atmosphere, and cloud height, and so will vary from place to place. Typically it will occur within a kilometer of the surface.< If this is true then the amount of CO2 presently in the air must absorb nearly all of the available IR radiation so how does more CO2 create more warming?
unspecial @107, the lapse rate refers only to the change in atmospheric temperature with altitude. Of necessity, it has the same magnituderegardless of whether you measure it going up or going down. The lapse rate is the response to decreased pressure with altitude based on the ideal gas law as modulated by the addition of more heat either by differential absorption of sunlight with altitude (as in the stratosphere) or by the release of latent heat from condensing water vapour. The geothermal gradient is the change of temperature with depth of the Earth's rocks and soil. It is a function of the temperature difference between the core and surface as modulated by the thermal conductivity of the rocks. Other than determining the rate at which geothermal energy reaches the surface, the geothermal gradient has very little impact on climate.
With regard to your three questions:
1) Yes it does, although its effect in that regard is minor relative to that of H2O. Further, it reduces the daily temperature range (diurnal temperature range) by increasing the heat capacity of the atmosphere as well as by the absorption of outgoing IR radiation.
2) In hypothetical situations, water is not always a part of the equation. Because its concentration in the atmosphere depends on atmospheric temperature, and also the extent of exposed liquid water, at very cold temperatures, its effect is negligible. Absent CO2, the atmospheric temperatures fall to levels where the effect of H2O is near negligible, and is certainly much reduced from its current effect.
Clouds rise or fall for a variety of reasons, none of which are related to age. The most common cause of the rise and fall of clouds would be updrafts or downdrafts in the atmosphere. Further the condensing of water releases heat within clouds, often generating powerful updrafts. That is what causes the formation of cumulo-nimbus clouds in which the base is not raised, but the upper level of the cloud is lifted to the tropopause. Clearly the evaporation of water droplets in clouds will have the reverse effect, but because the water is evaporating, the cloud diminishes in size so and may disappear, so the effect is not as noticable.
3) As explained in the OP, the greenhouse effect is not a function of where IR radiation is first absorbed when it leaves the Earth's surface, but of the altitude from which it is radiated to space. Chris Colose shows the following graph:
The graph plots temperature (x-axis) versus altitude (y-axis), with the diagonal lines representing the lapse rate. The horizontal line at H represents an initial "effective altitude of radiation to space" which is a sort of average of the altitudes from which the various IR photons actually reaching space are emitted. (Technically, it is that altitude in the troposphere with the such that a black body at that temperature would emit as much power to space as IR radiation as is actually observed.)
If you increase the CO2 concentration, some of the IR radiation emitted going upward from H would be absorbed by that additional CO2, then re-emitted at a higher, cooler location in the atmosphere. The effect is to raise the effective altitude of radiation to space to ΛH (pronounced "lambda H". Because the energy balance between incoming SW radiation and outgoing IR radiation must be preserved, that will result in changes that raise the temperature a ΛH to the previous temperature of H. Those temperature changes will then propogate to the Earth's surface due to the constant lapse rate, raising the surface temperature by the same as the rise in temperature at ΛH relative to its previous value. The rise in temperature equals (ΛH-H) x Γ, where "Γ" (the capital greek letter gamma) represents the lapse rate.
If the change in CO2 concentration at the surface results in an increase of back radiation that would otherwise cause a greater change in temperature than (ΛH-H) x Γ, it will result in increased convection, reducing the temperature change back to that value. If it would have resulted in less of a temperature change than (ΛH-H) x Γ, it will result in reduced convection, increasing the temperature to that value. Consequently, to a reasonable estimate (and you will not do better without a full fledged climate model) the change in absorption at the surface can be ignored. It is the change of emission height that matters.
cdbenny elsewhere, using Wein's displacement law (or a convenient calculator) you can indeed determine that the peak intensity of a black body with a temperature of 193 K is 15.1 micrometers. However, using Planck's Law (or a convenient calculator) you will quickly determine that the radiation intensity at any wavelength always increases with increasing temperature. As the point of peak intensity moves to a shorter wavelength, the intensity of the longer wavelengths still increases. Thus, at 193 K, the intensity at 15.1 micrometers is 1.0967 W*m-2*µm-1*sr-1. At 288 K, it is 5.7595 W*m-2*µm-1*sr-1, or 5.25 times more intense. At 6000 K it is 881.53 W*m-2*µm-1*sr-1, or 153 times more intense than at the Global Mean Surface Temperature. This relationship, for temperatures relevant in the atmosphere of Earth, can be seen in the graph below.
6000 K is approximately the Sun's surface temperature. But, of course, although the Sun radiates at 15.1 K far more intensely than at the Earth's surface, the Sun's radiation at the Earth's surface is much diminished. Indeed, at its peak it is diminished by the ratio of the Sun's surface area to the area of a sphere having the radius of the distance of the Earth from the Sun. That is, it is diminished by a factor of 0.00009. Ergo, the incomeing IR radiation from the Sun at the Earth peaks at 1.4% of the intensity of the outgoing radiation from the Earth's surface. (This is important, because if it averaged a the same magnitude, there could be no greenhouse effect.)
The upshot is the 15 micrometer absorption band of CO2 absorbs a significant proportion of the outgoing radiation from the Earth's surface (as can be seen in the diagram above), but an inconsequential amount of the incoming radiation from the Sun.
Further, the actual amount absorbed by CO2 can be inconsequential to the greenhouse effect. What is more important is the average temperature at which the heat stored in the CO2 is radiated. That heat can come from collisions with other molecules and does not need to be specifically absorbed by the CO2 molecule that radiates it (see OP above). Consequently, although CO2 is responsible for 20% of the total greenhouse effect, it probably absorbs less than 20% of IR radiation that is absorbed by the atmosphere.
Curtis @109: Your last paragraph "...IR absorbed by CO2 can be inconsequential...more important is avg.temp at which the heat stored in CO2 is radiated. That heat can come from collisions with other molecules (convection) and does not need to be specifically absorbed by CO2."
All the molecules in the atm radiate, say at 288K, O2,N2,H2O,CO2,Ar, and would cool at same rate, and maintain same temp (convection). The 'heat stored' in 200ppmv CO2, represented by its heat capacity, is abt 1/4,800th Joules/K compared to the rest of the atm components. So, if IR absorbed by CO2 'can be inconsequential' why is CO2 more-or-less important than the other atm components? (It is understandable that IR absorbed by CO2 can be inconsequential if it is very, very low energy.)
@110: 2nd para., 2nd line; "...and maintain same temp (convection) at any particular elevation (say 1 meter delta).
cdbenny
"All the molecules in the atm radiate, say at 288K, O2,N2,H2O,CO2,Ar, and would cool at same rate"
Incorrect. Only the GH gases - H2O & CO2 in your list - radiate in the infrared. O2, N2 and Argon can't radiate in the infrared - being symmetrical molecules (or atoms in the case of Argon) they are unable to generate a charge separatrion across the molecule and thus can't support emission or absorption of IR photons.
Radiation by gases is a very different process from radiation by solids or liquids. The main driver of what is going on once absorption has occurred is collisions. Absorbing molecules transfer the energy they have absorbed to other molecules around them through collisions.
And potential emitting molecules are energised to then be able to emit through collisions with non-emitting molecules.
cdbenny @110, here is a graph of radiation intensity of a 'black body' (in this case a bolt of ligtning):
As the graph shows, Wien's Displacement Law determines the temperature of a black body from the wavelength of peak radiation, or the wavelength of peak radiation for the the black body radiation at a given temperature. It does not tell you the radiation intensity at that or any other point on the curve. That is determined by Planck's Law. Nor does it tell you the total radiation emitted (ie, the area under the curve). That is determined by the Stefan-Boltzmann Law.
Gases are not black bodies. They do not radiate at every wavelength. Rather, they radiate at specific wavelengths determined by the nature of their chemical bonds (at medium and long wavelengths) and the atomic structure of their components (at short wavelengths). They absorb radiant energy only at the wavelengths at which they would radiate if hot enough. The result is a unique emission spectrum for every gas, as illustrated below:
Here are the absorptivities (and hence emissivities, by Kirchoff's Law) of a variety of gases across a range of frequencies relavent to atmospheric processes:
Returning to Planck's Law, it tells us that as the temperature of a black body increases, the intensity of the radiation from that black body increases at every wavelength. This can be seen in the graph below.
If a gas is hot enough to radiate, it will radiate at a given wavelength at an intensity given by the black body intensity at that wavelength (as determined by Planck's Law) multiplied by the emissivity at that wavelength (as shown in the chart above). That means the wavelength of peak emission may not coincide with either the wavelength of peak emission of a black body (as shown by Wien's Law) or the wavelength of peak emissivity. Instead it is both a function of the intensity of black body at each wavelength and emissivity at each wavelength. Thus even though the emissivity of CO2 at aproximately 2.5 and 4 micrometers is just as great as that at 15 micrometers, at normal Earth temperatures radiation from those wavelengths is inconsequential, while that at 15 micrometers dominates.
Where the Earth's atmosphere warmer than 15000 K, so that the peak blackbody radiation occured at wavelengths of approximately 2 micrometers, far more energy emitted from CO2 would come from the 2.4 and 4 micrometer bands than the 15 micrometer bands. Fortunately for us, the atmosphere is much cooler than that and the 15 micrometer band dominates, but the only significance Wien's Displacement Law has with regard to that fact is that the peak radiation for atmospheric temperatures occurs around 20 micrometers, not around 5 micrometers.
Combining these facts together, the fact that the wavelength of peak emission for CO2 coincides with the wavelength of peak radiation for a black body at 193 K is pure coincidence, and tells us nothing about the intensity of the radiation of CO2. This is clearly demonstrated by the back radiation from Barrow (on the north coast of Alaska) and Nauru, as shown below. The radiation intensity at 15 micrometers is from CO2. It is far more intense from the warmer Nauru than it is from Barrow. In both, in fact at 15 micrometers it approximately coincides black body curve for the surface temperature at the location. In Nauru, on the 15th of November, 1998, it readiates at a black body temperature of 300K at 15 micrometers, whereas at Barrow on the 10th of March, 1999, it radiates at a black body temperature of slightly less than 245 K at 15 micrometers (due to a temperature inversion).
In sum, the idea that CO2 radiation is "very, very low energy" because of the wavelength of its primary radiation is shere nonsense. At best it reflects abysmal ignorance for which there cannot be any possible further excuse.
Further, while it is true that all molecules in the atmosphere radiate at 288K, the intensity of radiation of all but the greenhouse gases is inconsequential relative to that of CO2 at that temperature, even allowing for relative abundances. Further, the radiation at 15 micrometers is inconsequential relative to that of CO2 for all atmospheric gases other than H2O. As it happens, because H2O is far more abundant than CO2 at temperate and tropical surface temperatures, and because it absorbes strongly at far more wavelengths, most radiative absorption in the lower atmosphere will be by H2O. That, however, is irrelevant to the greenhouse effect because the energy is transferred to CO2 by collision, and because at high altitudes, CO2 is far more abundant than H2O, and it is the cool temperature of CO2 radiating to space (and hence from high altitudes) that determines the strength of the greenhouse effect.
[PS]I could be wrong but I suspect cdbenny may think that GHE is largely about warming of gases in atmosphere and missing backradiation to surface. ie see introduction here.
So, you suppose personal insults are appropriate?(..sheer nonsense, ..abysmal ignorance). I am just looking for answer to question: "How much energy, Joules/year, is 200ppmv CO2 responsible for adding to earth environment/atmosphere?"
[JH] Argumentative remarks are not acceptable on this website. Please keep it civil.
cdbenny
See here. Select panel 2 in the slide show.
That is heat accumulation in the top 2000 meters of the ocean. The largest build up of heat in the system, around 93%
By eyeball that is about 1.5 * 10^22 joules last year. That is due to the sum off the factors changing the climate of which CO2 is the biggest contributor.
To put that number into context, it is a rate of over 450 trillion watts. In contrast total human energy consumption is at around 18 trillion watts and total geothermal heat flows from within the Earth are at around 47 trillion watts.
cdbenny @114, the question is nonsensical. If you change the CO2 concentration there will be a change in the energy flux to space. If the change is a decrease from 280 ppmv to 200 ppmv, it will result in a greater flow of energy to space; while if it is a change from 100 to 200 ppmv, it will result in a reduced flow of energy to space. In either case, the change in flow will gradually return to a value equal to and opposite in sign to the flow of energy from the Sun to Earth, at which time there will be equilibrium (averaged over a short period of years) and no net change in the quantity of energy at the Earth's surface.
Looking at your question, you ask for a rate (joules per year). So you are after a value where you need to specify an initial concentration and have not. Your question is therefore a version of "how long is a piece of string?" or "how deep is a hole?" or other such nonsense questions that only appear in jokes. But worse, even if you have an initial value, you are after a fixed value for a flux that changes over time, and where the change from the initial state tends to zero over time.
Further, you did not just ask a question. You repeatedly made nonsense claims about the greenhouse effect, and about the atmospheric absorption of CO2 which, among other confusions, revealed a deep misunderstanding of Wien's Law. Pointing out that these nonsense claims of yours are nonsense is not an insult. Only if I had no respect for intelligence would I be indifferent to the premises you use in argument - considering all equally valid. Your premises were sheer nonsense. Now, you can learn different and proceed accordingly (showing thereby intelligence and integrity); or not. In the later case, it is your response that condemns you - not my correctly pointing out that your premises were nonsense.
Glenn @115, that does not answer cdbenny's question, which was about a concentration of 200 ppmv of CO2, not an increase in concentration of 200 ppmv (which we have not experience yet in any event). But, yes, an ongoing increase, currently at 120 ppmv, is currently resulting in a 1.5*10^22 Joules per annum increase in surface energy, which is currently increasing because we are further increasing the CO2 concentration faster than the rate at which the surface temperature approaches the equilibrium value for the current concentration (at which point net energy flux would be zero).
Tom Curtis @117.
I think in treating cdbenny's question @114 literally, you are ignoring the assessment you made of the abilities of the questioner. His question as stated on first arrival @SkS was perhaps written with a little more care and is quite different. "For 220 ppmv man-made CO2 in Earth atmosphere, how much real energy does that amount of CO2 absorb from the Sun, or from 15 micro-meter wavelength IR radiated back from the Earth?" So this presumably concerns a level of CO2 elevated above the natural or pre-industrial level. I cannot think why the 220ppm value is chosen. Perhaps cdbenny could redeem himself by explaining. There is also the question of whether "amount absorbed" is literally that, or whether it is the 'amount absorbed and re-radiated back whence it came.'
Increase of 200-220 ppmv CO2 in earth atm since industrial rev is incorrect. SkS "CO2 History" chart shows increase from abt 280 to 400ppmv. Question in #114: How much energy, Joules/year, is 120 ppmv man-made CO2 responsible for adding to earth atm/environment; can that be determined from IR radiation 'not exiting atm'?
MA Rodger @118, specifically regarding the question, "For 220 ppmv man-made CO2 in Earth atmosphere, how much real energy does that amount of CO2 absorb from the Sun, or from 15 micro-meter wavelength IR radiated back from the Earth?" it is difficult to answer. Even if we clarrify the ambiguity as to whether it is asked how much 500 ppmv (280 preindustrial plus 220 anthropogenic) would absorb, or how much extra is absorbed by 500 ppmv relative to 280 ppmv, it is difficult to answer. That is because Line By Line radiation models, which would be used to answer that question, are designed to show the net upward and downward radiation at each level. They do not typically integrate total absorption over the whole atmospheric column. Instead, at each level they calculate the amount absorbed from the net upward (or downward) radiation from the next lowest level, and the amount emitted upward (and downward) from that level.
Further, they do not calculate the amount both emitted and absorbed within the same level, which constitutes a substantial fraction of the radiation, particularly at lower levels. Nor do they calculate the sidewards component of the emissions and absorptions (an even larger proportion of atmospheric absorption and emission) as they effectively cancel out. GCM's do calculate the sidewards component (but not the full spherical emissions and absorptions) but at a much coarser scale, thereby inflating the component of emissions and absorptions wihtin the same cell.
There are very good reasons for these limitations on LBL radiation models. The components that they do not calculate result in no net transfer of energy, and cannot be directly observed. In contrast, the components they do calculate do result in a net transfer of energy, and can be observed. As a result, they have been shown to be very accurate.
If we ask about the net transfer, we can answer the questions with LBL models (or more approximately with the University of Chicago's online Modtran model). Using the later, if we 0 all ghg components except CO2, and use the 1976 US Standard Atmosphere with no cloud, looking down from 70 Km we find total emissions of 358.274 W/m^2 with zero CO2, 325.618 W/m^2 with 280 ppmv, and 322.478 W/m^2 with 500 ppmv. That shows that the 280 ppmv absorbs approximately 33 W/m^2 more than it emits, vertically integrated in the upward direction. Increasing that to 500 ppmv results in both an increase in absorption and emission, but vertically integrated in the upward direction it absorbs approximately an additional 3.14 W/m^2 more than its increase in emissions.
Because of the vertical temperature profile of the atmosphere, while absorption dominates the net upward radiative energy flow, emission dominates the net downward energy flow. So, looking up from 0 Km, net emissions with no CO2 is 23.66 W/m^2, with 280 ppmv it is 82.205W/m^2 and with 500ppmv it is 87.606 W/m^2. Hence net downard emissions exceed net absorption of downward IR radiation by approximately 60 W/m^2 for 280 ppmv, and by an additional 5 W/m^2 for 500 ppmv.
Adding back the other GHG into the atmosphere will not change the total emission by CO2 (which is temperature dependant). It will result in a decrease in the net absorption relative to emission by CO2 as some of the absorption will be by other components. In particular, there is significant overlap between H2O and CO2. Overall, there will be an increase in net absorption relative to emission in the upward direction due to those additional components, and an increase in net emission relative to absorption in the downward direction.
Finally, to respond to another possible interepretation of the original question - at 280 ppmv, between 14.327 and 15.625 micrometers, all emissions from the surface are absorbed by CO2 (or CO2 and H2O in the actual atmosphere) before it reaches space, with the radiation to space in that band coming entirely from higher levels of the atmosphere. Increasing the atmospheric concentration to 500 ppmv increases the band of total absorption of surface radiation to 14.245 to 15.773 micrometers. The same bands will stop 100% of solar radiation in those wavelengths from reaching the surface.
cdbenny @119, that is a well phrased question. To answer, if there have been not feedbacks or temperature responses to the change (other than some rapid adjustements in the stratosphere) the reduction in energy leaving the troposphere by radiation for a change in CO2 concentration is 5.35 x ln(CO2/original CO2) +/-10%. The top of the troposphere is used for this calculation as it greatly increases the convenience of the calculation. LBL models, however, are validated against radiation to the specific height of the observing platform (most often satellites). For an increase from 280 to 400 ppmv, that amounts to 1.9 W/m^2 (or 3.06 x 10^22 Joules per annum for the whole surface of the Earth).
However, that is the change only prior to any temperature changes or feedback in the troposphere or at the surface. Conservation of energy will result in changes in the troposhere and at the surface that will reduce that temperature energy imbalance over time to zero. As temperature drives the feedbacks, that means there must be some increase in temperature, and there is very good reason to think the increase will be about 3 C per 3.7 W/m^2 energy imbalance (or 0.8 C per W/m^2) with a significant margin of error which is biased towards higher values.
Hello. I have a question from denialist that i can not answer (with my little brain).
It is about CO2/H2O absorbing/reflecting/reemitting infrared.
Earth reflects back infrared, it hits CO2/H20 (if there is cloud cover, it likely will happen in cloud cover but it could be lower/higher too). This warms up, warm air moves up by conevction and releases its energy (at least some of it would be done via infrared). Howevers the infrared now has less resistance when it gets emitted towards space. So the greenhouse gas layer (more dense, more humid) at lower levels will act now as a shield.
Am i on right track:
a) Before the convection makes warm air to release its energy high up, the energy in this 'warm air bubble' has already made surface/low atmosphere temperature to rise.
b) There is difference in infrared spectrum at lower atmosphere (where we should see smaller C02/H20 impact) and what it is when measured from space ("bigger" footprint in where CO2,H20 absorb it) - Doesnt this show that the heat at CO2/H20 frequencys gets trapped for more time (and hence warms all else up) in the atmosphere?
c) As molecules that get heated via infrared rise up, they loose some of the energy on the way via conduction and now if they happen to emit infrared, it is on a different frequency (so more potential for this infrared to heat up earth surface than get reflected by cloud cover or CO2 molecules)
RSaar @122,
Your description of the Greenhouse Effect rather exaggerates the role of convection. You will note the SkS OP above explaining the Greenhouse Effect makes no mention of convection whatever. Note also that the standard graphic representing energy flux through the atmosphere shows convective "Thermals" as being the smallest quantity under consideration.
The idea that atmospheric gas significantly cools the planet by circulating from the warm surface up to the upper troposphere where it sheds its heat to space is thus wrong. The atmosphere has very little vertical movement. To appreciate this, consider the big circulations which would provide this convection.
The Hadley Cells are but 15km high but stretch for 3,000km North-South. The horizontal flow we experience as wind would have to be massive, supersonic, to provide the gas in any quantity ready-warmed for its upward journey. Instead, winds are not so rapid and the average flow upwards through the troposphere is very gentle taking an average of about 2 weeks from bottom to top. (I am ignoring hurricanes in saying this. Tropical cyclones do provide a mechanism for rapid convective flow and do constitute a significant part of those "Thermals" 17W/m2.)
The absence of large convection cooling is because the atmosphere is pretty-much in balance. It is indeed cooler at altitiude but if a packet of air rises it expands with the reducing pressure and thus will cool and be no warmer than the gas it replaces. (Note this means your (c) is not correct. There is no conduction effect. The cooling results from the drop in pressure with height.)
I'm not sure where this leaves your question.
MA Rodger. In scenario where molecule absorbs infrared, then cools (say by losing some of its kinetic energy) and then re-emits infrared (it is likely to happen when background is cooler than given molecule), it is not going to be same wavelength? If it is so, could it be a wavelength that same type of molecules do not interact (can CO2 molecule emit infrared that it itself unable to absorb?).
RSaar @124,
You ask "it is not going to be same wavelength?"
The wavelength will remain the same. Note the vibrational energy from the absorbed IR photon can convert either into a re-emitted photon (which can go off any-which-way) or into kenetic energy within the gas. And kenetic energy collisions can result in vibration which again can be emitted as a photon or can return into the gas's kinetic energy. The difference that temperature makes is that lower temperatures result in less photons being emitted. The wavelength of the photons is unaltered. In simple terms, the wavelength is dictated by the mode of vibration in the molecule while the gas temperature will dictate the number of photons emitted. Thus (in simple terms) the higher (and colder) the gas at which CO2 becomes rare enough to give its emitted 15μm IR a clear run out into space (without it being blocked by CO2 higher in the atmosphere); the higher and colder that altitude, the less radiation there will be emitted out into space in that CO2 band and the less cooling provided to the planet.
Could somebody point me towards values of how long is the CO2 vibrational relaxation time, i have a note 10-16s range (i assume this is in 300K range, 1 atm pressure), but i have no idea from where i got this from or whether it is somewhat right.
At 15C, i calculate that there will be collisions (in N2 gas, but thats close enough) 2.8 x 109 s (using hyperphysics tool)
What i am hoping to show is that in lower atmosphere, the IR excited CO2 is likely to collide (and possibly give away its vibrational energy?( with other air molecules before it emits photon. Is that statement correct?
RSaar @126:
Yes. Without going into details (which I am too busy to look up at the moment), IR absorbed by CO2 is far more likely to be dissipated as heat energy into the atmosphere by collisions than be being reradiated, and this is true throughout the range of temperatures and pressures found in the troposphere.
However, it is important to realize is that, firstly, the average time to relaxation by reemission is just that, an average time. Sometimes it will occur much quicker, so that a small proportion is reradiated rather than dissipated through collisions.
Secondly, it is also important to realize that the distinct vibrational modes of CO2 associated with the absorption of IR radiation can also arise as a result of collisions. Indeed, within the range of tropospheric temperatures and pressures, they are more likely to arise from collision than from absorption of IR radiation. Most of the energy absorbed from collisions absorbed by CO2 in this manner will be dissipated by collisions, but some will reradiate. Indeed, the same proportion will dissipated as IR radiation as for energy absorbed by IR radiation. What is more, if the gas is at the same temperature as the source of the IR radiation (and ignoring reduction of intensity of radiation due to the inverse square law), the combined energy radiated from the ghg will equal the amount absorbed by the IR gas.
There is a specious denier argument that because of the dissipation of absorbed IR energy by collisions, the greenhouse effect cannot work, and ghg serve only to cool the atmosphere. It is much favoured by the Galileo Institute in Australia, among others. Their argument ignores the emission of thermal energy as IR radiation within the bulk of the atmosphere, but at the same time assumes its existence at the top of the troposphere to serve as a cooling effect. What is worse, if radiation actually worked as they (inconsistently) assume, the GHE would actually be stronger because no energy would escape from the lower or middle troposphere to space as radiation, with the net effect or further raising the effective altitude of radiation to space.
Thank you for the reply. Though not sure i can put this quote to context at all.
If the gas is at the same temperature as the source of the IR radiation (and ignoring reduction of intensity of radiation due to the inverse square law), the combined energy radiated from the ghg will equal the amount absorbed by the IR gas.
Air and earth being at same temp? Was this meant to say that against 3K cosmos, eventually all that absorbed from IR source (earth) gets emitted?
Hi Tom
Just to say that the link to MODTRAN above does not work:
http://forecast.uchicago.edu/Projects/modtran.doc.html
How about this one:
http://climatemodels.uchicago.edu/modtran/
[PS] Fixed link. Thanks for finding that.
RSaar:
This post over at Rabett Run gives a good explanation of the likelhood of CO2 losing energy by emission or collision. You will find it in agreement with what Tom Curtis said.
Air and earth are not at the same temperature - air temeprature generally decreases with height. If you look at surface net IR, it is overal a loss of energy from the surface, but the rate varies.
Outgoing IR is roughly estimated by the Stefan-Boltzman equation using surface temperature. (Surface is a very good, but not perfect emitter). It can 250, 300, 400 W/m^2 at a typical range of cold-to-warm temperatures.
Incoming IR from the atmosphere is not so easily estimated, as the atmosphere is a less efficient emitter and what arrives at the surface comes from a range of heights (and air temperatures). With low oevercast, it will be similar to outgoing IR - cluds are good emitters. In clear skies the incoming IR is substantially less than outgoing IR. A typcial range is for incoming IR to be anywhere from a few to 150 W/m^2 less than outgoing IR. This holds true over a wide range of surface temperatures.
RSaar @128, first I need to correct myself slightly. What I should have written is that:
In my original statement I had in mind only the outward radiation.
What this means is that if the temperature of the atmosphere was uniform, and the same as that at the surface, the outgoing IR radiation at the Top Of the Atmosphere (TOA) would be the same as the outgoing IR radiation at the surface. In fact, however, the temperature generally falls with altitude, and nearly always does in the thickest part of the atmosphere from which most outgoing radiation from the atmosphere originates (the troposphere). The consequence is that at those wavelengths where all, or nealy all of the upwelling IR from the surface is absorbed, the outgoing IR radiation from the atmosphere, which comes from a cooler source, is less than that from the surface. That is illustrated in the first graph from the OP (shown below):
Averaged across the entire Earth, the effect is that the upwelling IR radiation at the surface is significantly greater than the outgoing IR radiation at the TOA (consisting or upwelling IR radiation from the atmosphere, plus whatever IR radiation from the surface which was not absorbed by the atmosphere), and that difference is the greenhouse effect. The point of the OP is that this is directly a function of the temperature structure of the atmosphere. With equal temperatures there would be no greenhouse effect, and if the atmosphere were warmer than the surface, you would have a reverse greenhouse effect.
DEFINITION OF GREENHOUSE EFFECT
The greenhouse effect is a natural phenomenon, which helps to keep the earth’s surface warm and that is why life on earth is possible.
What is Greenhouse Effect ? is a simplequestion I thought