The anthropogenic global warming rate: Is it steady for the last 100 years? Part 2.
Posted on 7 May 2013 by KK Tung
This is part 2 of a guest post by KK Tung, who requested the opportunity to respond to the SkS post Tung and Zhou circularly blame ~40% of global warming on regional warming by Dumb Scientist (DS).
In this second post I will review the ideas on the Atlantic Multidecadal Oscillation (AMO). I will peripherally address some criticisms by Dumb Scientist (DS) on a recent paper (Tung and Zhou [2013] ). In my first post, I discussed the uncertainty regarding the net anthropogenic forcing due to anthropogenic aerosols, and why there is no obvious reason to expect the anthropogenic warming response to follow the rapidly increasing greenhouse gas concentration or heating, as DS seemed to suggest.
For over thirty years, researchers have noted a multidecadal variation in both the North Atlantic sea-surface temperature and the global mean temperature. The variation has the appearance of an oscillation with a period of 50-80 years, judging by the global temperature record available since 1850. This variation is on top of a steadily increasing temperature trend that most scientists would attribute to anthropogenic forcing by the increase in the greenhouse gases. This was pointed out by a number of scientists, notably by Wu et al. [2011] . They showed, using the novel method of Ensemble Empirical Mode Decomposition (Wu and Huang [2009 ]; Huang et al. [1998] ), that there exists, in the 150-year global mean surface temperature record, a multidecadal oscillation. With an estimated period of 65 years, 2.5 cycles of such an oscillation was found in that global record (Figure 1, top panel). They further argued that it is related to the Atlantic Multi-decadal Oscillation (AMO) (with spatial structure shown in Figure 1, bottom panel).
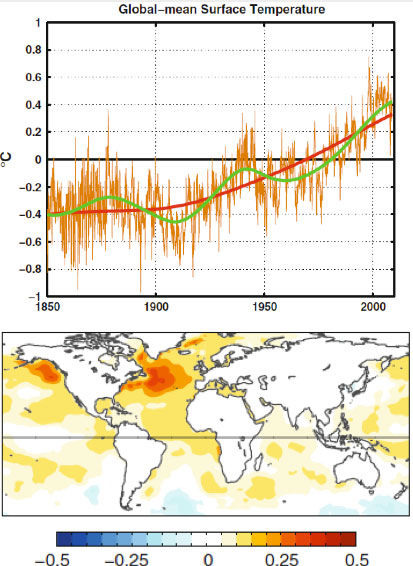
Figure 1. Taken from Wu et al. [2011] . Top panel: Raw global surface temperature in brown. The secular trend in red. The low-frequency portion of the data constructed using the secular trend plus the gravest multi-decadal variability, in green. Bottom panel: the global sea-surface temperature regressed onto the gravest multi-decadal mode.
Less certain is whether the multidecadal oscillation is also anthropogenically forced or is a part of natural oscillation that existed even before the current industrial period.
It is now known that the AMO exists in coupled atmosphere-ocean models without anthropogenic forcing (i.e. in “control runs”, in the jargon of the modeling community). It is found, for example in a version of the GFDL model at Princeton, and the Max Planck model in Germany. Both have the oscillation of the right period. In the models that participated in IPCC’s Fourth Assessment Report (AR4), no particular attempt was given to initialize the model’s oceans so that the modeled AMO would have the right phase with respect to the observed AMO. Some of the models furthermore have too short a period (~20-30 years) in their multidecadal variability for reasons that are not yet understood. So when different runs were averaged in an ensemble mean, the AMO-like internal variability is either removed or greatly reduced. In an innovative study, DelSol et al. [2011] extract the spatial pattern of the dominant internal variability mode in the AR4 models. That pattern (Figure 2, top panel) resembles the observed AMO, with warming centered in the North Atlantic but also spreading to the Pacific and generally over the Northern Hemisphere (Delworth and Mann [2000] ).
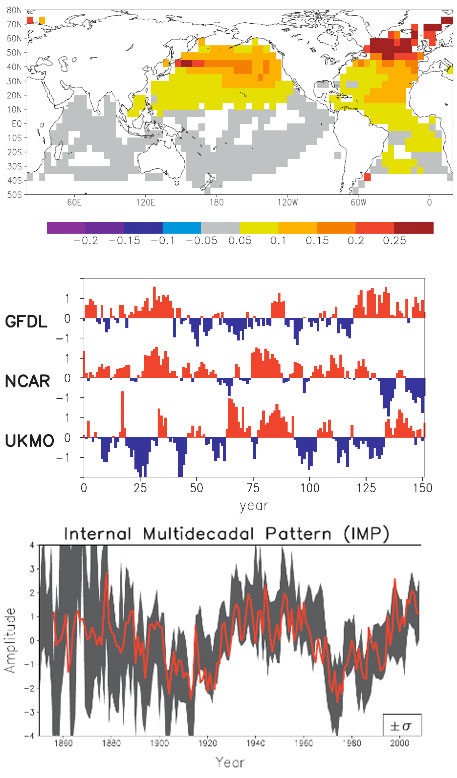
Figure 2. Taken from DelSol et al. [2011] . Top panel: the spatial pattern that maximizes the average predictability time of sea-surface temperature in 14 climate models run with fixed forcing (i.e. “control runs”). Middle panel: the time series of this component in three representative control runs. Bottom panel: time series obtained by projecting the observed data onto the model spatial pattern from the top panel. The red curve in the bottom panel is the annual average AMO index after scaling.
When the observed temperature is projected onto this model spatial pattern, the time series (in Figure 2 bottom panel) varies like the AMO Index (Enfield et al. [2001] ), even though individual models do not necessarily have an oscillation that behaves exactly like the AMO Index (Figure 2, middle panel).
There is currently an active debate among scientists on whether the observed AMO is anthropogenically forced. Supporting one side of the debate is the model, HadGEM-ES2, which managed to produce an AMO-like oscillation by forcing it with time-varying anthropogenic aerosols. The HadGEM-ES2 result is the subject of a recent paper by Booth et al. [2012] in Nature entitled “Aerosols implicated as a prime driver of twentieth-century North Atlantic climate variability”. The newly incorporated indirect aerosol effects from a time-varying aerosol forcing are apparently responsible for driving the multi-decadal variability in the model ensemble-mean global mean temperature variation. Chiang et al. [2013] pointed out that this model is an outlier among the CMIP5 models. Zhang et al. [2013] showed evidence that the indirect aerosol effects in HadGEM-ES2 have been overestimated. More importantly, while this model has succeeded in simulating the time behavior of the global-mean sea surface temperature variation in the 20th century, the patterns of temperature in the subsurface ocean and in other ocean basins are seen to be inconsistent with the observation. There is a very nice blog by Isaac Held of Princeton, one of the most respected climate scientists, on the AMO debate here. Held further pointed out the observed correlation between the North Atlantic subpolar temperature and salinity which was not simulated with the forced model: “The temperature-salinity correlations point towards there being a substantial internal component to the observations. These Atlantic temperature variations affect the evolution of Northern hemisphere and even global means (e.g., Zhang et al 2007). So there is danger in overfitting the latter with the forced signal only.”
The AMOC and the AMO
The salinity-temperature co-variation that Isaac Held mentioned concerns a property of the Atlantic Meridional Overturning Circulation (AMOC) that is thought to be responsible for the AMO variation at the ocean surface. This Great Heat Conveyor Belt connects the North Atlantic and South Atlantic (and other ocean basins as well), and between the warm surface water and the cold deep water. The deep water upwells in the South Atlantic, probably due to the wind stress there (Wunsch [1998] ). The upwelled cold water is transported near the surface to the equator and then towards to the North Atlantic all the way to the Arctic Ocean, warmed along the way by the absorption of solar heating. Due to evaporation the warmed water from the tropics is high in salt content. (So at the subpolar latitudes of the North Atlantic, the salinity of the water could serve as a marker of where the water comes from, if the temperature AMO is due to the variations in the advective transport of the AMOC. This behavior is absent if the warm water is instead forced by a basin wide radiative heating in the North Atlantic.) The denser water sinks in the Arctic due to its high salt content. In addition, through its interaction with the cold atmosphere in the Arctic, it becomes colder, which is also denser. There are regions in the Arctic where this denser water sinks and becomes the source of the deep water, which then flows south. (Due to the bottom topography in the Pacific Arctic most of the deep water flows into the Atlantic.) The Sun is the source of energy that drives the heat conveyor belt. Most of the solar energy penetrates to the surface in the tropics, but due to the high water-vapor content in the tropical atmosphere it is opaque to the back radiation in the infrared. The heat cannot be radiated away to space locally and has to be transported to the high latitudes, where the water vapor content in the atmosphere is low and it is there that the transported heat is radiated to space.
In the North Atlantic Arctic, some of the energy from the conveyor belt is used to melt ice. In the warm phase of the AMO, more ice is melted. The fresh water from melting ice lowers the density of the sinking water slightly, and has a tendency to slow the AMOC slightly after a lag of a couple decades, due to the great inertia of that thermohaline circulation. A slower AMOC would mean less transport of the tropical warm water at the surface. This then leads to the cold phase of the AMO. A colder AMO would mean more ice formation in the Arctic and less fresh water. The denser water sinks more, and sows the seed for the next warm phase of the AMO. This picture is my simplified interpretation of the paper by Dima and Lohmann [2007] and others. The science is probably not yet settled. One can see that the physics is more complicated than the simple concept of conserved energy being moved around, alluded to by DS. The Sun is the driver for the AMOC thermohaline convection, and the AMO can be viewed as instability of the AMOC (limit cycle instability in the jargon of dynamical systems as applied to simple models of the AMOC).
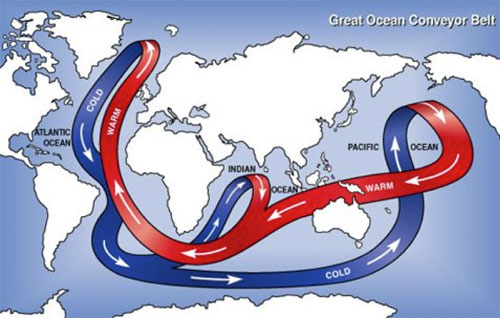
Figure 3. The great ocean conveyor belt. Schematic figure taken from Wikipedia.
Preindustrial AMO
It is fair to conclude that no CMIP3 or CMIP5 models have successfully simulated the observed multidecadal variability in the 20th century using forced response. While this fact by itself does not rule out the possibility of an AMO forced by anthropogenic forcing, it is not “unphysical” to examine the other possibility, that the AMO could be an internal variability of our climate system. Seeing it in models without anthropogenic forcing is one evidence. Seeing it in data before the industrial period is another important piece of evidence in support of it being a natural variability. These have been discussed in our PNAS paper. Figure 4 below is an updated version (to include the year 2012) of a figure in that paper. It shows this oscillation extending back as far as our instrumental and multi-proxy data can go, to 1659. Since this oscillation exists in the pre-industrial period, before anthropogenic forcing becomes important, it plausibly argues against it being anthropogenically forced.
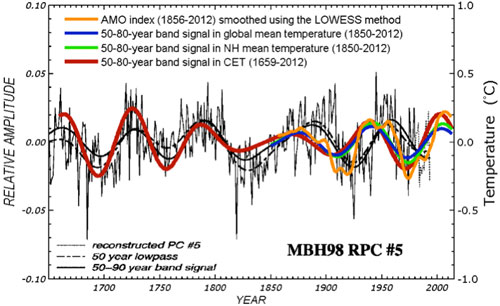
Figure 4. Comparison of the AMO mode in Central England Temperature (CET) (red) and in global mean (HadCRUT4) (blue), obtained from Wavelet analysis, with the multi-proxy AMO of Delworth and Mann [2000] (in thin black line). The amplitude of multi-proxy data is only relative (left axis). The orange curve is a smoothed version of the AMO index originally available in monthly form.
The uncertainties related to this result are many, and these were discussed in the paper but worth highlighting here. One, there is no global instrumental data before 1850. Coincidentally, 1850 is considered the beginning of the industrial period (the Second Industrial Revolution, when steam engines spewing out CO2 from coal burning were used). So pre-industrial data necessarily need to come from nontraditional sources, and they all have problems of one sort of the other. But they are all we have if we want to have a glimpse of climate variations before 1850. The thermometer record collected at Central England (CET) is the longest such record available. It cannot be much longer because sealed liquid thermometers were only invented a few years earlier. It is however a regional record and does not necessarily represent the mean temperature in the Northern Hemisphere. This is the same problem facing researchers who try to infer global climate variations using ice-core data in the Antarctica. The practice has been to divide the low-frequency portion of that polar data by a scaling factor, usually 2, and use that to represent the global climate. While there has been some research on why the low-frequency portion of the time series should represent a larger area mean, no definitive proof has been reached, and more research needs to be done. We know that if we look at the year-to-year variations in winters of England, one year could be cold due to a higher frequency of local blocking events, while the rest of Europe may not be similarly cold. However, if England is cold for 50 years, say, we know intuitively that it must have involved a larger scale cooling pattern, probably hemispherically wide. That is, England’s temperature may be reflecting a climate change. We tried to demonstrate this by comparing low passed CET data and global mean data, and showed that they agree to within a scaling factor slightly larger than one. England has been warming in the recent century, as in the global mean. It even has the same ups and downs that are in the hemispheric mean and global mean temperature (see Figure 4).
In the pre-industrial era, the comparison used in Figure 4 was with the multiproxy data of Delworth and Mann [2000]. These were collected over geographically distributed sites over the Northern Hemisphere, and some, but very few, in the Southern Hemisphere. They show the same AMO-like behavior as in CET. CET serves as the bridge that connects preindustrial proxy data with the global instrumental data available in the industrial era. The continuity of CET data also provides a calibration of the global AMO amplitude in the pre-industrial era once it is calibrated against the global data in the industrial period. The evidence is not perfect, but is probably the best we can come up with at this time. Some people are convinced by it and some are not, but the arguments definitely were not circular.
How to detrend the AMO Index
The mathematical issues on how best to detrend a time series were discussed in the paper by Wu et al. [2007] in PNAS. The common practice has been to fit a linear trend to the time series by least squares, and then remove that trend. This is how most climate indices are defined. Examples are QBO, ENSO, solar cycle etc. In particular, similar to the common AMO index, the Nino3.4 index is defined as the mean SST in the equatorial Pacific (the Nino3.4 region) linearly detrended. Another approach uses leading EOF in the detrended data for the purpose of getting the signal with the most variance. An example is the PDO. One can get more sophisticated and adaptively extract and then subtract a nonlinear secular trend using the method of EMD discussed in that paper. Either way you get almost the same AMO time series from the North Atlantic mean temperature as the standard definition of Enfield et al. [2001] , who subtracted the linear trend in the North Atlantic mean temperature for the purpose of removing the forced component. There were concerns raised (Trenberth and Shea [2006 ]; Mann and Emanuel [2006] ) that some nonlinear forced trends still remain in the AMO Index. Enfield and Cid-Serrano [2010] showed that removing a nonlinear (quadratic) trend does not affect the multidecadal oscillation. Physical issues on how best to define the index are more complicated. Nevertheless if what you want to do is to detrend the North Atlantic time series it does not make sense to subtract from it the global-mean time variation. That is, you do not detrend time series A by subtracting from it time series B. If you do, you are introducing another signal, in this case, the global warming signal (actually the negative of the global warming signal) into the AMO index. There may be physical reasons why you may want to define such a composite index, but you have to justify that unusual definition. Trenberth and Shea [2006] did it to come up with a better predictor for a local phenomenon, the Atlantic hurricanes. An accessible discussion can be found in Wikipedia. http://en.wikipedia.org/wiki/Atlantic_multidecadal_oscillation
The amplitude of the oscillatory part of the North Atlantic mean temperature is larger than that in the global mean, but its long-term trend is smaller. So if the global mean variation is subtracted from the North Atlantic mean, the oscillation still remains at 2/3 the amplitude but a negative trend is created. K.a.r.S.t.e.N provided a figure in post 30 here. I took the liberty in reposting it below. One sees that the multidecadal oscillation is still there. But the negative trend in this AMO index causes problems with the multiple linear regression (MLR) analysis, as discussed in part 1 of my post.
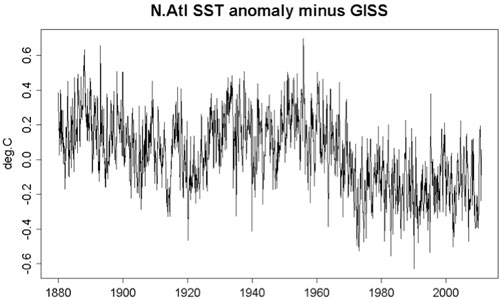
Figure 5: North Atlantic SST minus the global mean.
From a purely technical point, the collinearity introduced between this negative trend in the AMO index and the anthropogenic positive trend confuses the MLR analysis. If you insist on using it, it will give a 50-year anthropogenic trend of 0.1 degree C/decade and a 34-year anthropogenic trend of 0.125 degree C/decade. The 50-year trend is not too much larger than what we obtained previously but these numbers cannot be trusted.
One could suggest, qualitatively, that the negative trend is due to anthropogenic aerosol cooling and the ups and down due to what happens before and after the Clean Air Act etc. But these arguments are similar to the qualitative arguments that some have made about the observed temperature variations as due to solar radiation variations. To make it quantitative we need to put the suggestion into a model and check it against observation. This was done by the HadGEM-ES2 model, and we have discussed above why it has aspects that are inconsistent with observation.
The question of whether one should use the AMO Index as defined by Enfield et al. [2001] or by Trenberth and Shea [2006] was discussed in detail in Enfield and Cid-Serrano [2010] , who argued against the latter index as “throwing the baby out with the bath water”. In effect this is a claim of circular argument. They claimed that this procedure is valid “only if it is known a priori that the Atlantic contribution to the global SST signal is entirely anthropogenic, which of course is not known”. Charges of circular argument have been leveled at those adopting either AMO index in the past, and DumbScientist was not the first. In my opinion, the argument should be a physical one and one based on observational evidence. An argument based on one definition of the index being self-evidently correct is bound to be circular in itself. Physical justification of AMO being mostly natural or anthropogenically forced needs to precede the choice of the index. This was what we did in our PNAS paper.
Enfield and Cid-Serrano [2010] also examined the issue of causality and the previous claim by Elsner [2006] that the global mean temperature multidecadal variation leads the AMO. They found that the confusion was caused by the fact that Elsner used a 1-year lag to annualized data: While the ocean (AMO) might require upwards of a year to adjust to the atmosphere, the atmosphere responds to the ocean in less than a season, essentially undetectable with a 1-year lag. The Granger test with annual data will fail to show the lag of the atmosphere, thus showing the global temperature to be causal.
What is an appropriate regressor/predictor?
There is a concern that the AMO index used in our multiple regression analysis is a temperature response rather than a forcing index. Ideally, all predictors in the analysis should be external forcings, but compromises are routinely made to account for internal variability. The solar forcing index is the solar irradiance measured outside the terrestrial climate system, and so is a suitable predictor. Carbon dioxide forcing is external to the climate system as humans extract fossil fuel and burn it to release the carbon. Volcanic aerosols are released from deep inside the earth into the atmosphere. In the last two examples, the forcing should actually be internal to the terrestrial system, but is considered external to the atmosphere-ocean climate system in a compromise. Further compromise is made in the ENSO “forcing”. ENSO is an internal oscillation of the equatorial Pacific-atmosphere system, but is usually treated as a “forcing” to the global climate system in a compromise. A commonly used ENSO index, the Nino3.4 index, is the mean temperature in a part of the equatorial Pacific that has a strong ENSO variation. It is not too different than the Multivariate ENSO Index used by Foster and Rahmstorf [2011] . It is in principle better to use an index that is not temperature, and so the Southern Oscillation Index (SOI), which is the pressure difference between Tahiti and Darwin, is sometimes used as a predictor for the ENSO temperature response. However, strictly speaking, the SOI is not a predictor of ENSO, but a part of the coupled atmosphere-ocean response that is the ENSO phenomenon. In practice it does not matter much which ENSO index is used because their time series behave similarly. It is in the same spirit that the AMO index, which is a mean of the detrended North Atlantic temperature, is used to predict the global temperature change. It is one step removed from the global mean temperature being analyzed. A better predictor should be the strength of the AMOC, whose variation is thought to be responsible for the AMO. However, measurements deep ocean circulation strength had not been available. Recently Zhang et al. [2011] found that the North Brazil Current (NBC) strength, measured off the coast of Brazil, could be a proxy for the AMOC, and they verified it with a 700-year model run. We could have used NBC as our predictor for the AMO, but that time series is available only for the past 50 years, not long enough for our purpose. They however also found that the NBC variation is coherent with the AMO index. So for our analysis for the past 160 years, we used the AMO index. This is not perfect, but I hope the readers will understand the practical choices being made.
References
Booth, B. B. B., N. J. Dunstone, P. R. Halloran, T. Andrews, and N. Bellouin, 2012: Aerosols implicated as a prime dirver of twentieth-century North Atlantic climate variability. Nature, 484, 228-232.
Chiang, J. C. H., C. Y. Chang, and M. F. Wehner, 2013: Long-term behavior of the Atlantic interhemispheric SST gradient in the CMIP5 historial simulations. J. Climate, submitted.
DelSol, T., M. K. Tippett, and J. Shukla, 2011: A significant component of unforced multidecadal variability in the recent acceleration of global warming. J. Climate, 24, 909-026.
Delworth, T. L. and M. E. Mann, 2000: Observed and simulated multidecadal variability in the Northern Hemisphere. Clim. Dyn., 16, 661-676.
Elsner, J. B., 2006: Evidence in support of the climatic change-Atlantic hurricane hypothesis. Geophys. Research. Lett., 33, doi:10.1029/2006GL026869.
Enfield, D. B. and L. Cid-Serrano, 2010: secular and multidecadal warmings in the North Atlantic and their relationships with major hurricane activity. Int. J. Climatol., 30, 174-184.
Enfield, D. B., A. M. Mestas-Nunez, and P. J. Trimble, 2001: The Atlantic multidecadal oscillation and its relation to rainfall and river flows in the continental U. S. Geophys. Research. Lett., 28, 2077-2080.
Foster, G. and S. Rahmstorf, 2011: Global temperature evolution 1979-2010. Environmental Research Letters, 6, 1-8.
Huang, N. E., Z. Shen, S. R. Long, M. L. C. Wu, H. H. Shih, Q. N. Zheng, N. C. Yen, C. C. Tung, and H. H. Liu, 1998: The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. London Ser. A-Math. Phys. Eng. Sci., 454, 903-995.
Mann, M. E. and K. Emanuel, 2006: Atlantic hurricane trends linked to climate change. Eos, 87, 233-244.
Trenberth, K. E. and D. J. Shea, 2006: Atlantic hurricanes and natural variability in 2005. Geophys. Research. Lett., 33, doi:10.1029/2006GL026894.
Tung, K. K. and J. Zhou, 2013: Using Data to Attribute Episodes of Warming and Cooling in Instrumental Record. Proc. Natl. Acad. Sci., USA, 110.
Wu, Z. and N. E. Huang, 2009: Ensemble empirical mode decomposition: a noise-assisted data analysis method. Adv. Adapt. Data Anal., 1, 1-14.
Wu, Z., N. E. Huang, S. R. Long, and C. K. Peng, 2007: On the trend, detrending and variability of nonlinear and non-stationary time series. Proc. Natl. Acad. Sci., USA, 104, 14889-14894.
Wu, Z., N. E. Huang, J. M. Wallace, B. Smoliak, and X. Chen, 2011: On the time-varying trend in global-mean surface temperature. Clim. Dyn.
Wunsch, C., 1998: The work done by the wind on the oceanic general circulation. J. Phys. Oceanography, 28, 2332-2340.
Zhang, D., R. Msadeck, M. J. McPhaden, and T. Delworth, 2011: Multidecadal variability of the North Brazil Current and its connection to the Atlantic meridional overtuning circulation. J. Geophys. Res.,, 116, doi:10.1029/2010JC006812.
Zhang, R., T. Delworth, R. Sutton, D. L. R. Hodson, K. W. Dixon, I. M. H. Held, Y., J. Marshall, Y. Ming, R. Msadeck, J. Robson, A. J. Rosati, M. Ting, and G. A. Vecchi, 2013: Have aerosols caused the observed Atlantic Multidecadal Variability? J. Atmos. Sci., 70, doi:10.1175/JAS-D-12-0331.1.































 Arguments
Arguments






























Mod: please delete #99. Dunno why it came out empty...
#46 scaddenp at 08:54 AM on 17 May, 2013
"MS1 "I think their paper failed " really?... If the ENSO index was substantially flawed or there was significant non-linearity, this isnt born out by the success of their prediction. If you believe that the prediction can be improved significantly by other indexes or method, then show us."
---------------------
Compo et al 2010 have addressed this issue.
http://www.esrl.noaa.gov/psd/people/gilbert.p.compo/CompoSardeshmukh2008b.pdf
"Because its [ENSO's] spectrum has a long low frequency tail, fluctuations in the timing, number and amplitude of individual El Nino and La Nina events, within, say, 50-yr intervals can give rise to substantial 50-yr trends..."
"...it also accountd for an appreciable fraction of the total warming trend..." (see figure 9b )
"...It [The Pacific decadal oscillation or the interdecadal Pacific oscillation] is strongly reminiscent of the low-frequency tail of ENSO and has, indeed been argued to be such in previous studies (e.g. Alexander et al 2002, Newman et al 2003, Schneider and Cornuelle 2005, Alexander et al 2008)..."
"...In this paper, we have argued that identifying and removing ENSO-related variations by performing regressions on any single ENSO index can be problematic. We stressed that ENSO is best viewed not as a number but as an evolving dynamical process for this purpose..."
I think this confounds physical and statistical modelling but I will look at the paper. The success of more recent techniques (like F&R) would strongly suggest that this paper is mistaken. The indices might be an imperfect measure of the large scale process, but they are good enough for predicting unforced variation in global temperature due to ENSO.
KK Tung @97.
The thesis we discuss (Tung & Zhou 2013) specifically addresses multidecadal episodes of warming and cooling. This "hiatus period" you now discuss has been evident within the temperature record for less than a decade. Given the present short duration of this "hiatus period," given the many other points presented within Tung & Zhou 2013, is it helpful to our discussion to introduce yet another topic into this discussion? Indeed, why is the "hiatus period" relevant?
So far the two posts on this thesis have encompassed (1a) The shape of the net anthorpogenic forcing profile. (1b) Sea ice as a driver of AMO, (2a) AMO in climate models. (2b) AMOC evidence. (2c) Pre-industrial AMO data. (2d) Remnant anthropogenic signal in AMO. (2e) Using AMO as a "forcing."
So far, most of these topics remain poorly addressed, if addressed at all. I would suggest adding a fresh item to this discussion (ie introducing the "hiatus period" ) which does not appear entirely relevant is the opposite of what we should be attempting.
MA Rodger It seems to me that Prof. Tung has introduced the "hiatus" largely as a way of establishing the existence of internal variability, although I think the majority of SkS readers will already accept that without the need for it to be stated explicitly.
Prof Tung writes
Yes, I think that the majority of SkS readers would agree that the ensemble mean is probably the best method we currently have for estimating the forced response of the climate system and that any difference between the observations and the ensemble mean can be explained as being due to the unforced response due to sources of internal climate variability. This is of course, provided the difference is approximately within the spread of the ensemble (in reality this is probably an underestimate of the true uncertainty due to the small number of model runs and the limited number of models).
I do not agree with this statement. There are multiple sources of internal climate variability, which include for example ENSO and plausibly AMO. Most of the time these will be acting to warm or cool the climate essentially at random, and so most of the time might be expected to largely cancel out. This is why the ensemble mean, while being an estimate of only the forced response, is still a reasonable point estimate of the observed climate. However, sometimes multiple sources of internal variability may temporarily align in direction, causing the observed climate to stray away from average conditions. Under such circumstances one would expect the observations to stay reasonably close to the forced response most of the time, but for there to be occasional periods of little or no warming, or conversely more warming than expected.
Easterling and Wehner (2009) investigated this issue in some detail and found that
In other words, we should expect to see the occasional "hiatus" ocurr due to internal climate variability, the models predict that they will happen if you wait long enough, but being chaotic phenomena the models cannot predict when they will happen. As far as I can see, there is little evidence that the models need internal variability more in recent years than they did before.
It is also worth noting that the issue to do with baselines may look as if the observations were more central in the spread of the models during the baseline period as baselining removes any offset between timeseries exactly within the baseline period, but only approximately outside. Some of these offsets will be due to random rather than systematic differences, so the apparent uncertainty of the models in the baseline period will be lower than outside the baseline period. This effect will be smaller the longer the baseline period, as shown in my earlier post, but I suspect it does contribute to the observations looking less "anomalous" during the pre 2000 years than perhaps they should.
I think it is very important to be highly skeptical of phenomenon that seem obvious from a visual inspection of the data. The human eye is very prone to seeing patterns in noise that don't actually mean anything. We should be reticent in claiming that there has been a real hiatus until there is statistically significant evidence for that assertion.
Incidentally, as Dumb Scientist points out, I have also made two posts in the previous thread addressing the issue of circularity, which seems to suggest that the regression method proposed does involve circularity. The posts are here and here. If you are a MATLAB user, I can send you the scrips used to perform the analysis.
In reply to post 106 by Dikran: The effect of offsetting on the perceived spread of models has been underdiscussed in literature. I agree with what you said about it here, and I would encourage you to develop it into a publishable paper. The procedure of offsetting with a baseline is needed for model projections because projection is different from a prediction. In a prediction of ,say weather for the next few days, today's measured weather is our baseline, and such a baseline is assimulated into the model. The model attempts to predict both the forced and unforced response. Due to chaos, models start to deviate after today, and after two weeks, the prediction becomes mostly useless. But it is useful for a week or so.
The IPCC projections of future climate change is different. The model is initiated in the preindustrial period, 1850-1870, runs about 150 years in the 20th century simulation (when what is to be simulated is known), and then runs forward under different scenarios of future emissions. There is no hope of doing a prediction of both the forced and unforced response over such a long period. Instead it is hoped that the forced response of the climate is simulated with the ensemble mean of the model runs. If, in the presentation of the results, all models are offset against their initial condition at 1850-1870. The intermodel spread is rather large, even during the period of 20th simulation, where the observed response is known before hand. This is caused by systematic errors in each model. This intermodel spread is reduced by offsetting each model's ensemble mean by its own climatology in a specified period, say 1980-1999, as used in Chapter 10 of AR4. It reduced the intermodel spread during the period of offset, and also for a decade or so after that. AR4 uses different offsetting period in different chapters, and there is no consensus on how to do it. You have found that a longer offsetting period makes the pre-2000 results less anomalous. On the other hand, for the purpose of evaluating projections to the future, perhaps it may be fairer to the models to offset it with the lates known data. That is, year 2000 for AR4 projection and year 2005 for the CMIP5 projection. We however do not know what the observed forced response is, but since AR4 models have simulated the observed 20th warming quite well with forced (ensemble mean) solutions, it may not be a bad idea to offset the model prediction at year 2000 for AR4 projection with the observation at year 2000, and then attribute the subsequent deviation of the model ensemble mean from the observation to the presence of internal variability. Have you tried it yet?
Regarding the Matlab code result of Dikran mentioned in post 106 and by DumbScientist earlier:
I am frustrated that I have not been able to get my point across despite a few attempts, as you continue to focus on a technical procedure, the multiple linear regression analysis (MLR). As I discussed in part 2 of the post, the MLR analysis follows the arguments laying out the evidence in favor of the AMO being mostly natural. The MLR is then used to see the possible impact it may have on the deduced anthropogenic warming rate assuming that the AMO is mostly natural. The MLR analysis cannot stand on its own as evidence. If that were what we did in our PNAS paper, then our arguments would have indeed been circular.
I also mentioned in part 2 of my post that one could legitimately claim that use of either the Enfield AMO index or the Trenberth and Shea index is ciruclar, if that is the entirety of the evidence that you presented. Similarly, as you have done here, you assume the hypothetical case that the AMO is anthropogenically forced, but you do a MLR assuming it is instead mostly natural and remove it. You can then demonstrate that the resulting anthropogenic response is wrong. That is, it is different than you originally assumed to be true. Conversely, if you consider the hypothetical case that the AMO is mostly natural, but you do not remove it, you would also get a wrong anthropogenic response in the end. This you could have known even before you do the Matlab calculation.
Dr. Tung - I would agree that the identification of the AMO is critical for attribution analysis. I would disagree on the AMO index you used.
You used the CET as an AMO proxy - however the CET is equally vulnerable to aliasing (hiding) the global warming signal. Frequency analysis in this case is suspect, as the sum forcings in the 20th century (GISS forcings here), when averaged out by climate response times, have a frequency similar to that of the AMO observations - and are therefore not directly separable using just time series analysis.
---
I am in addition greatly disappointed that you have (as yet) failed to respond to my points regarding the Ting et al 2009 analysis (time/spatial principal component analysis supporting the Trenberth Shea 2006 detrending method, not linear detrending) or to ocean heat content thermodynamic constraints (upper limits on contributions from internal variation), as raised here. Either of these points indicate a much different anthropogenic contribution to current temperatures.
Again, I don't think that's the issue. Removing the AMO to determine anthropogenic warming would only be justified if detrending the AMO from 1856-2011 actually removed the trend due to anthropogenic warming.
Those arguments aren't sufficient to support your claim that ~40% of the warming over the last 50 years can be attributed to a single mode of internal variability. Especially because Isaac Held and Huber and Knutti 2012 used thermodynamics to conclude that all modes of internal variability put together couldn't be responsible for more than about 25% of the warming.
Actually, Dikran's analysis defines the AMO as 40% anthropogenic and 60% natural. So it is mostly natural.
But again, I think the key point is that linear detrending doesn't remove the nonlinear anthropogenic trend from the AMO.
In reply to post 104 on the relevance of the recent hiatus to the present thread on the Tung and Zhou (2013) paper: That paper offered one possible explanation for the observed hiatus observed since 2005, as due to a recurrent internal variability. Therefore it is relevant (thank you, Dikran, for pointing this out in post 105). There are many other suggestions, including coal burning in the emergent economy of China (Kaufmann et al. [2011] ), increases in stratospheric water (Solomon et al. [2010] ), or increases in “background” stratospheric aerosol (Solomon et al. [2011] ). I in no time suggested that ours is the only explanation. The most recent explanation is that the heating from the greenhouse gas induced radiative imbalance goes into the deep ocean. There are two timely paper by Jerry Meehl and his co-workers: One is published in 2011 in Nature Climate Change,vol 1, page 360-364, entitled : "Model based evidence of deep ocean heat uptake during surface temperature hiatus periods". The other is currently under consideration at J. Climate, entitled "Externally forced and internally generated decadal climate variability associated with the Interdecadal Pacific Oscillation". They are very relevant to our current thread.
Meehl et al used CCSM4 model run with a future scenario (RCP4.5), which does not have oscillatory variations in the forcing or dips such as those by volcano eruptions. With smooth forcing, the 5-member ensemble mean model global mean temperature is also smoothly increasing. However the individual members show variability about the mean of around 0.5 K from peak to trough. These papers are not about how good the model is in comparison with observation.
From an energy balance standpoint, the top of the atmosphere radiative imbalance driven by the anthropogenic forcing should be accounted for mostly by the heat uptake in the oceans, as land and ice have much lower heat capacity. In the model this heat budget can be done exactly. Meehl et al defined the hiatus period as when the surface temperature has a negative trend even in the presence of increasing radiative driving. They found that during the hiatus period, the composite mean shows that the upper ocean takes significantly less heat whereas the ocean below 300m takes up significantly more, as compared with the non-hiatus period. The second paper compares hiatus periods with accelerated warming periods, and finds the opposite behavior: the upper ocean takes up more heat and the deeper ocean much less.
The question is, what causes some periods to have more heat going into the deep ocean while some other periods the heat staying more in the upper ocean? I suggest that this is caused by the internal variability that we were discussing earlier. Our previous exchanges hopefully established the viewpoint that we should view the ensemble mean as the forced solution and the deviations from the ensemble mean by each member as internal variability. There are no hiatus periods in the forced solution under the CCSM4 RCP4.5 experimental setup. In fact this solution is smoothly increasing in its global mean temperature. It is the internal variability, possibly associated with variations in the deep overtuning circulations in the oceans, which determines when a portion of the heat should go to the deep ocean and show up as warming hiatus, and when it should stay near the surface, and show up as accelerated warming. ENSO, which we generally view as internal variability, also has this kind of vertical distribution variability in the oceans: In La Nina, the upper ocean is cool while the heat goes to the deeper ocean, and opposite behavior in El Nino.
The CCSM4 is known to have internal variability that is faster than in the observation. Instead of having hiatus periods of about 2-3 decades in the observation its cooling periods last 1-2 decades. This may possibly be caused by too rapid a vertical mixing in the ocean but I do not know for sure. The Interdecadal Pacific Oscillation (IPO) that was discussed by Meehl et al is the low frequency portion of the Pacific Decadal Oscillation (PDO). In the observation the IPO cooling periods coincides with the cooling periods of the AMO, which led me to suspect that the IPO is just the Pacific manifestation of the AMO, which is caused by the variations of the Atlantic Meridional Overturning Circulation.
KK Tung @111.
Thank you for pointing out the mention of the 'hiatus' in T&Zh13. It had passed me by. The actual quote is:-
In the first post here at SkSci, there was also the statement that the residuals following MLR with QCO2(t) function showed "a minor negative trend in the last decade" ie during this same 'hiatus' period'. Indeed, is this "minor negative trend" as shown in fig 3 of the first post not the 'hiatus' iself that remains unexplained by T&Zh13 when the actual AMO is used (although explained with a theoretical "recurrent" AMO.)?
Prof Tung, regarding your most recent post: As I said, I think SkS readers are familiar with the idea of internal variability and would readily agree that internal variability is most likely the cause of the apparent hiatus. However, the abstract of your paper in JAS makes the claim that:
This is advancing a much stronger claim than that the hiatus is mot likely due to internal variability, but that some of the action of AMO has been misattributed to anthropogenic forcing. The only quantative support for this assertion seems to come from the regression model. In my example on the other thread I have shown that this regression model is flawed, and if AMO actually doesn't affect global mean surface temperatures (in your notation, the correct value of the regression coefficient D is precisely zero), then the regression method can misattribute some of the effects of anthropogenic forcing to the AMO.
In an earlier post, Prof. Tung wrote:
The MLR analysis is clearly the key element of the paper in JAS entitled "Deducing Multidecadal Anthropogenic Global Warming Trends Using Multiple Regression Analysis". For that paper to be sound, it is incumbent on you to be able to refute the counter example I have provided that shows the method is unreliable.
Enfield and Trenberth & Shea would only be circular if they used their detrended AMO indices to deduce the anthropogenic influence on global temperatures. There is nothing circular about detrending AMO to remove anthropogenic influence, the circularity is introduced by assuming a model of anthropogenic warming to detrend AMO and then using that detrended AMO to deduce the anthropogenic warming.
No, this is clearly not the case. In my example the AMO signal is a mixture of anthropogenic and natural. The point is that the detrending procedure, whether lienar or quadratic affects both the anthropogenic and natural components of the AMO signal. As a result the detrended AMO can still act as a proxy for anthropogenic warming, either because the detrending model was incorrect (in the case of lienar detrending) or becase the natural component is correlated with the anthropogenic signal (in the case of quadratic detrending).
The whole purpose of using a synthetic example is that I know that the resulting anthropogenic response is wrong as I know what the correct answer is by construction. The MLR method gives the wrong answer unless the AMO is detrended to remove the anthropogenic signal exactly, which can't be done unless you know what the anthropogenic signal is a-priori.
The AMO signal in my example is mostly natural. If the MLR method is sound, it needs to work whether the AMO is strongly affected by anthropogenic factors or not, and whether AMO affects global surface tempertures or not.
It is very important that you provide me with a direct answer to this question, so we can focuss in on the area of disagreement quickly: Ignoring for the moment whether the hypothetical scenario is appropriate, is there an error in my implementation of the MLR method? "Yes" or "No", if "Yes", please explain.
In reply to post 113 by Dikran: The MLR analysis was used in our paper to investigate the impact on the deduced anthropogenic trend of a mostly natural AMO, with the latter being related to the classically defined AMO index by Enfield. As I said in an earlier post, the technical analysis related to MLR should not stand on its own: it merely tests the consequence of an assumption of one variable on another. Even in Zhou and Tung (2013, JAS), which is a more technical paper dealing with a comparison of the MLR analysis by three groups, there was a whole section, section 4, justifying introducing the AMO index as a regressor. (And the part of the Abstract that you quoted is out of context.)
Nevertheless I still think your exercise is useful in helping to think through the consequences of different scenarios. You should probably come up with a better example because the one you used has a technical problem which may mar the point you were trying to make. The point you were trying to make is apparently important to this group of readers and so I would encourage that you fix that technical problem. The technical problem is that the AMO that you defined is 40% of one regressor and 60% of another regressor, and so you ran into a serious problem of collinearity. I think your point could be made without this distraction.
There are several scenarios/assumptions that one could come up with. These, when fully developed, can each stand on its own as a competing theory. I had in many occasions mentioned that there are competing theories to ours and referenced the ones that appeared in the literature that I knew of. I accepted these as valid competing theories explaining the same phenomenon of the observed climate variability. One fully developed competing theory is that of Booth et al arguing that the entire AMO-like variability is forced by anthropogenic aerosols varying in like fashion. One could also come up with one that says that 50% of this observed variability is forced by anthropogenic aerosol. A third one that says only 20% is caused by anthropogenic aerosol forcing. The first two scenarios could probably be checked by the subsurface ocean data of Zhang et al (2013). The available observational data with their short subsurface measurements and uncertainty are probably not able to discriminate the third scenario from the one that assumes that the AMO is natural.
We can in our thought experiment move closer to the ones that you may be thinking. Consider the scenario where the two cycles in the AMO index, classically defined, in the global mean data is natural but the most recent half cycle starting in 1980 is anthropogenically forced. Therefore the accelerated warming in the latter part of the 20th century is entirely anthropogenically forced. This is a fully developed competing theory, in fact the standard theory. It is fully developed because it has been simulated by almost all CMIP3 models (compare AR4 figure 9.5 a and b). There is no need for internal variability to explain the accelerated warming between 1980 and 2005; the accelerated warming is attributed to accelerated net radiative forcing driven by the exponentially (or super-exponentially) increasing greenhouse gas concentrations in the atmosphere. If we assume that this scenario is true, it would contradict our assumption that the AMO is mostly natural . If you perform a MLR and remove the AMO as natural, the deduced anthropogenic trend would be wrong. In this case it would be an underestimate of the true anthropogenic trend. Putting it in your language of linear vs nonlinear detrending, this scenario is equivalent to the assumption that the anthropogenic warming trend is highly nonlinear and bends rapidly up after 1980. And the wrong (by definition) assumption of a natural AMO can also be viewed as the procedure of linear detrending being wrong. I have said it previously you do not need a Matlab code to reach that conclusion. It is obvious.
Most would have been satisfied with the standard theory, except for what happened during the last decade or so. Although the year 2012 was the warmest on record for the contiguous US, according to NOAA’s National Climate Data Center, it was only the 9th or 10th warmest globally, depending on which dataset is used. The warmest global mean year was either 1998 (according to HadCRU) or 2005 (according to GISS). The year 2010 effectively tied with 2005. The warming in 1998 was rather spikey, and could be attributed to a “super” El Niño in 1997/1998, while the peak near 2005 was broader, indicating a top in the multidecadal variability sometime between 2005 and 2010. Under reasonable emission scenarios the projected warming by the IPCC models continues to rise rapidly after 2005. The observation now appears to be below the 95% variability bar of the CMIP3 model projections made in 2000 and on the lower edge of the 90% bar of CMIP5 projections made in 2005. Explaining this hiatus is one of the current challenges. Some of us proposed that it would be explained by a multidecadal variability, while I readily accepted the fact that there are other competing explanations.
If you have a competing theory, I would encourage you to develop it further. The example you used, with a quadratic trend in anthropogenic warming, does not appear to be consistent with observation, although I understand that you did not intend it to be used that way. The point I am trying to make is that one can come up with a dozen scenarios. When each is developed enough for publication it is open for critical examination by all. However, the technical arguments concerning MLR are probably beside the point.
Prof. Tung wrote:
No, the validity of MLR is providing evidence for your argument is central to the point.
As I pointed out, the MLR analysis is the central topic of the JAS paper, so it is important to investigate whether it is valid or not.
My thought experiment demonstrates that the MLR method is unable to perform this test for the reasons stated in my earlier post.
It is not a distraction. The colinearity is the extreme case of correlation between anthropogenic and AMO signals. It is common in thought experiments to investigate the boundary cases. For the MLR method to be a valid test it must work whether or not the AMO actually affects global mean surface temperatures or not, and it needs to be valid whether the AMO is heavily correlated with anthropogenic forcings or not. My analysis shows that it isn't valid as it misattributes anthropogenic influences to the AMO, which undermines the conclusion drawn in the JAS paper.
In my previous post I asked:
It is rather dissapointing that you did not give a direct answer to this simple question and instead commented only on the scenario. Please can you answer this question in order to avoid further miscommunication?
Prof. Tung wrote:
I have already presented an analysis showing that this statement is simply incorrect.
Do you stand by this statement, yes or no? If yes, please explain the error in the analysis.
In my original post, I claimed that regressing global temperatures against the linearly-detrended Atlantic Multidecadal Oscillation (AMO) to determine anthropogenic global warming (AGW) assumes that AGW is linear. Thus, even if AGW actually were faster after 1950, Dr. Tung's method would conclude that AGW is linear anyway.
Dr. Tung dismissed Dikran Marsupial's MATLAB simulation because its conclusion is "obvious" and suggested coming up with a better example without technical problems. I disagree with this criticism and would like to again thank Dikran for his contribution, which inspired this open-source analysis written in the "R" programming language.
Can regressing against the linearly-detrended AMO detect nonlinear AGW?
Imagine that AGW is very nonlinear, such that the total human influence on surface temperatures (not the radiative forcing) is a 5th power polynomial from 1856-2011:
t = 1856:2011
human = (t-t[1])^5
human = 0.8*human/human[length(t)]
Its value in 2011 is 0.8°C, to match Tung and Zhou 2013's claim that 0.8°C of AGW has occurred since 1910. The exponent of "5" was chosen such that the linear trend after 1979 is 0.17°C/decade, to match Foster and Rahmstorf 2011.
Tung and Zhou 2013 describes an AMO with an amplitude of 0.2°C and a period of 70 years which peaks around the year 2000:
nature = 0.2*cos(2*pi*(t-2000)/70)
Global surface temperatures are caused by both, along with weather noise described by a gaussian with standard deviation 0.2°C for simplicity:
global = human + nature + rnorm(t,mean=0,sd=0.2)
N. Atlantic sea surface temperatures (SST) are a subset of global surface temperatures, with added regional noise with standard deviation 0.1°C:
n_atlantic = global + rnorm(t,mean=0,sd=0.1)
Compare these simulated time series to the actual time series. The AMO is linearly-detrended N. Atlantic SST:
n_atlantic_trend = lm(n_atlantic~t)
amo = n_atlantic - coef(summary(n_atlantic_trend))[2,1]*(t-t[1])
Regress global surface temperatures against this AMO index and the exact human influence, after subtracting means to insure that the intercept handles any non-zero bias:
human_p = human - mean(human)
amo_p = amo - mean(amo)
regression = lm(global~human_p+amo_p)
Will Dr. Tung's method detect this nonlinear AGW? Here are the residuals:
Let's add the residuals back as Dr. Tung does, then calculate the trends after 1979 for the true and estimated human influences:
Note that the absolute values are meaningless. A Monte Carlo simulation of 1000 runs was performed, and the estimated human trends since 1979 are shown here:
Notice that even though we know that the true AGW trend after 1979 is 0.17°C/decade, Dr. Tung's method insists that it's about 0.07°C/decade. That's similar to the result in Tung and Zhou 2013, even though we know it's an underestimate here.
The linearity of the estimated human influence was measured by fitting linear and quadratic terms over 1856-2011 to the same 1000 runs. The same procedure applied to the true human influence yields a quadratic term of 5.965E-05°C/year^2.
Even though we know that the true quadratic term is 5.965E-05°C/year^2, the average quadratic term from Dr. Tung's method is less than half that. The true nonlinearity of this AGW term is 5th order, so this is a drastic understatement.
Conclusion: Tung and Zhou 2013 is indeed a circular argument. By subtracting the linearly-detrended AMO from global temperatures, their conclusion of nearly-linear AGW is guaranteed, which also underestimates AGW after ~1950.
In reply to KR at post 83 and originally at post 14 on the Anderson et al 2012 paper: It was claimed by KR that this paper has ruled out the possibility of more than 10% of the observed warming as contributed by natural variability. I am delinquent in replying to this thread.
Nothing of the sort--- that sets an upper limit of 10% as contributed by natural variability as claimed--- can be concluded from the model results.
Unlike the papers of Meehl et al that I discussed in post 113, the models used in Anderson et al are atmosphere-only, and are incapable of generating internal variability involving ocean dynamics. Through clever experimental design, the authors were able to place some constraints on the magnitude of unknown internal variability, and showed consistency within models which simulated well the observed warming of the late 20th century as almost entirely forced. In the first simulation, the observed sea-surface temperature (SST) in 1950-2005 is specified but with no greenhouse gas forcing or any other atmospheric forcing. In the second simulation, known atmospheric forcing such as greenhouse gases, tropospheric sulfate aerosols, tropospheric ozone and solar variations are added to the first. In third simulation, there is no change in SST. The atmospheric radiative forcing is the same as the second simulation. Five ensemble members are run for each experimental setup. The top-of-the atmosphere radiative imbalance is assumed to be the same as what should have been going into the (missing) ocean as change in ocean heat content. This is a reasonable assumption. The second simulation should give the radiative imbalance produced by known radiative forcing agents and the observed historical SST. This imbalance was compared with the ocean heat content change and was found to be in good agreement. The ocean heat content change was estimated using Levitus et al’s data up to 2008, and down to about 700m. It was assumed that this is 70% of the total ocean heat content, as the latter was not in the data. Possible errors associated with this one assumption alone already could exceed 10%. (This is however not my main argument.) The rest of the paper went on to argue why there is no room for more than 10% contribution from other unknown radiative forcing agents.
The model result should be viewed as a consistency test of the hypothesis proposed. As I mentioned in my previous posts, most CMIP3 models succeeded in simulating the observed warming in the second half of the 20th century as forced response using known radiative forcing agents with the magnitudes that they input into their models. If, as we argued in our paper and in part 1 of my post, the tropospheric aerosol cooling, which is uncertain, was underestimated, there would be a need for the presence of internal variability that warms during the second half of the 20th century. The authors acknowledged the possibility of two alternative hypotheses that were not tested by their work: My comments in bold below.
It should be noted that….there are two alternate, untested hypotheses. One is that the known change in total radiative forcing over the last half of the twentieth century … is systematically overestimated by the models (yes, that is our hypothesis) and that the long-term observed changes in global-mean temperatures are instead being driven by an unknown radiative-forcing agent(the unknown agent is the additional tropospheric sulfate aerosol cooling). The second hypothesis is that the global-scale radiative response of the system … is systematically underestimated by the models (equivalently the climate sensitivity is systematically overestimated) (I do not intend to argue that the climate sensitivity should be lower than used by the models, and so this is not the hypothesis that we pursued)…. However, for either of these two alternate hypotheses to supplant the current one (i.e., that known historical changes in total radiative forcing produced the observed evolution of global-mean SSTs and ocean heat content), the unknown forcing agent would need to be identified(we have identified it), changes in its magnitude would need to be quantified (we have not done it yet but showed what it needed to be), and it would have to be demonstrated that either (i) changes in the magnitude of known forcing agents in the model systems are systematically over-estimated by almost exactly the same amount or (ii) the radiative responses in the model systems are systematically underestimated by almost exactly the same amount. (Perhaps the word "exactly" should not be used in this context). However, testing either of these two hypotheses given the current model systems is not feasible until a candidate unknown forcing agent is identified and its magnitude is quantified.
Dr. Tung - Indeed, Anderson et al 2012 used atmospheric only models - examining integrated TOA deltas into the atmosphere against exchanges with the ocean surface and to some extent land surface and cryosphere (Anderson et al 2012 pg. 7166). They estimated OHC changes from those deltas, "...recognizing that the observed value may underestimate the total earth energy storage by 5%–15% (Levitus et al. 2005; Hansen et al. 2005; Church et al. 2011)." While an argument from input/output of the atmospheric climate layer has its limitations, it also has its strengths in that both TOA imbalance via spectroscopic evidence and SST values are quite well known.
They then evaluate estimated OCH changes against TOA inputs, concluding that <10% of global temperature change can be attributed to internal variations - as a boundary condition evaluation. I would also note that Andersons conclusions regarding "unknown forcings" such as aerosols limit their influence to no more than 25% of recent global temperature change - not the 40% you assert.
Your arguments against that paper (and by extension against Isaac Held and Huber and Knutti 2012) seem to me to require that either (a) climate sensitivity is badly estimated, in contradiction to the paleo evidence, or that (b) radiative forcings from basic spectroscopy are incorrect - as otherwise Andersons results hold.
If you wish (as stated above) to claim that "...the known change in total radiative forcing over the last half of the twentieth century … is systematically overestimated by the models", that would be (IMO) an entirely different paper, one with a considerable focus on spectroscopy and evidence regarding forcings (black carbon, atmospheric constitution, aerosol evidence, cloud trends). That is not the paper under discussion - and I (personal opinion, again) do not feel the current work holds up without such support.
And as I have stated (repeatedly, with what I consider insufficient objections) in this thread, the linear AMO detrending you use is (as Dikran has pointed out) critical to your conclusions - and that linear detrending is strongly contraindicated by recent literature, including some you have quoted in your support. That is entirely separate from the thermodynamics; two significant issues that argue against your conclusions.
In reply to post 115 by Dikran Marsupial:I appreciated your willingness to invest the time to code up the Matlab code and run the case you constructed in your post 57. You continue to focus on the technical issues. I owe you a technical answer. As far as we can tell, there is nothing wrong with your code and the procedure. However, you neglected to report the error bars of the your result. Without that information, you cannot legitimately conclude that the MLR underestimated the true value. This is an area that is your expertise, I believe, and so my explanation below is only for those readers who are not familiar with statistics or uncertainties in parameter estimation: one is comparing two quantities, A and B. A is the true value and B is the estimate of A. Since there is uncertainty in the estimate, B is often given in the form of b+/-c, with b being the central value and c being two standard deviations that defines the 95% confidence level for the estimate B. B is said to contain the true value A with 95% confidence if A lies within the range b-c to b+c.
In my post 114 commenting on your post 57, I mentioned that your artificially constructed case of an AMO that is 40% the same as the anthropogenic response is problematic because you have created a problem of collinearity between the two regressors In your multiple linear regression (MLR). The degree of collinearity matters because its effect shows up in the MLR result in the size of the error bars in the parameter estimates that MLR produces.
Since you did not provide them, we have recreated your code and reran it to produce the error bars. Your MLR model is:
Observation=b(1)*one+b(2)*anthro+b(3)*natural+b(4)*AMOd+ noise.
The b's are the elements in your vector beta. From one simulation we get b(1)=0.1364+/-0.0154, b(2)=0.6241+/-0.9336, b(3)=0.2155+/-2.1516 and b(4)=1.4451+/-3.3582. Note that these error bars are often larger than their central values. Ignoring b(1), which is the regression coefficient for the constant offset, the other b's are the estimates for anthro, natural and AMO, respectively. The true values for them, 1,1 and 0 are within the error bars of the estimate by MLR. So could should not have concluded that they are different.
Since you used a random noise model in your model, each simulation will be somewhat different from the other and from the one set of values that you reported in post 57. We repeated the simulation 10,000 times with different realizations of noise. We can report that 95% of the time the 95% confidence level includes the true value.
In conclusion, the MLR is giving you the correct estimate of the true value of anthropogenic response within the 95% confidence level range. Such a range is large in your case because of the serious collinearity of the model you constructed. In the MLR analysis of the real observation the degree of collinearity is much smaller, hence our error bars are much smaller, and so our MLR analysis gave useful results while your artificially constructed case did not yield useful results.
I will also try to reply to Dumb Scientist's post in a day or two. The problem of collinearity in his case is even more severe.
Minor correction to my post 120: " confidence level" should be "confidence interval".
The last sentence is confusing and should be deleted. I will explain in more detail on Dumb Scientist's post in a separate post.
In reply to post 116 by Dikran Marsupial: My previous attempt at posting a figure on AR4 projection was not successful. A gentleman at Skeptical Science offered to host my figures for me but needed clear copyright for the figurs. I do not currently have the time to search to ascertain the copyright. May I send it to you privately? Or we can wait for me to have more time.
I am no longer confident that my MATLAB programs actually do repeat the analysis in the JAS paper, at least it is difficult to reconcile the explanation given in Prof. Tung's first SkS post with the description in the paper (although the description in the paper seems rather vague).
It seems to me that the actual regressors used are: ENSO, volcanic, linearly detrended AMO and a linear trend acting as a proxy for anthropogenic forcing. So I shall modify my thought experiment accordingly.
Again, let us perform a simulation of 150 years
T = (1:150)';where again the anthropogenic forcing is quadratic, rather than linear
anthro = 0.00002*(T + T.^2);
and the effect of known natural forcings and variability (other than AMO) is sinusoudal
natural = 0.1*sin(2*pi*T/150);
As before, the observations are a combination of natural and anthropogenic forcings, but does not depend on AMO in any way
observations = anthro + natural + 0.1*randn(size(T));
Instead, AMO is a consequence of temperature change, rather than a cause
AMO = 0.4*anthro + 0.5*natural;
We can use regression to estimate the true linear rate of warming due to anthropogenic forcing
X = [ones(size(T)), T];
[beta,betaint] = regress(anthro, X);
which we find to be 0.03 +/- 0.001 degrees K per decade.
Again, we linearly detrend the AMO signal, in order to remove the anthropogenic component.
X = [ones(size(T)), T];
beta = regress(AMO, X);
AMOd = AMO - beta(2)*T;
Next, lets perform the regression exercise:
X = [ones(size(T)) natural-mean(natural) AMOd-mean(AMOd) T-mean(T)];
[beta,beta_ci,residual] = regress(observations, X);
model = X*beta;
The model provides a good fit to the data:
The regression coefficient for AMOd is 2.7685 +/- 1.2491, note that this interval DOES NOT contain the true value, which is zero.
The regression coefficient for the linear trend is 0.0011 +/- 0.0010, which does not contain the 'true' value of the linear trend due to anthropogenic emissions (0.003).
Following the procedure, we add on the residual to the linear component, and compare it with what we know to be the true anthropogenic influence:
deduced_anthro = X(:,4)*beta(4) + residual;
we can also calculate the deduced anthropogenic trend
X = [ones(size(T)), T];
[beta,betaint] = regress(deduced_anthro, X);
Note that the residuals have no appreciable trend, so this step does not solve the problem. The deduced anthropogenic trend is less than the true value, and the true value does not lie within the confidence interval.
Now one of the reasons for this failure is that not all of the anthropogenic component of AMO is removed by linear detrending. If we look at the deduced anthropogenic signal (green) we can see that it is rising approximately linearly, rather than quadratically like the true anthropogenic signal (red). The reason for this is simple, the quadratic part of the anthropogenic signal remains in the detrended AMO signal. This means that when we regress the observations on AMOd, AMOd can 'explain' the quadratic part of the anthropogenic forcing on the observations, so it doesn't appear in the residuals.
In reply to post 117 by Dumb Scientist: I have to admire your single-minded determination to "prove" that the result in Tung and Zhou (2013) somehow had a technical flaw. You had created a highly unrealistic case and tried to demonstrate that the Multiple Linear Regression (MLR) method that we used gives an underestimate of the true anthropogenic trend most of the time. Before we start I need to reiterate the basic premise of parameter estimation: if A is the true value and B is an estimate of A but with uncertainty, then B should not be considered to underestimate or overestimate A if A is within the 95% confidence interval (CI) of B. I previously discussed this problem in my post 120 addressing Dikran Marsupial's MLR analysis in his post 57.
Not taking CI of the estimate into account is not the only problem in your post 117. A more serious problem is your creation of an almost trivial example for the purpose of arguing your case. Your synthetic global temperature (denoted "global") is fine. It contains a smooth accelerated warming time series (denoted "human"), a smooth sinusoidal natural variation of 70 year period (denoted "nature"), plus a random noise, which contains year-to-year variations:
global=human+nature+rnorm(t,mean=0,sd=0.2)
Your synthetic North Atlantic temperature (denoted "n_atlantic") is exactly the same as "global" but for a small "regional" noise of standard deviation of 0.1, half of that of global mean:
n_atlantic=global+rnorm(t,mean=0,sd=0.1)
I said this is an almost trivial example because if this small "regional" noise were zero it would have been a trivial case (see later). Even with the small regional noise, your n_atlantic is highly correlated with your global data at higher than 0.8 correlation coefficient at all time scales. This is unrealistic because it is highly unlikely that a high frequency noise in North Atlantic also appears in the global mean. For example, a blocking event that makes Europe warmer in one year should not show up in the global mean. This defect is caused by the fact that each wiggle in the global noise also shows up in your n_atlantic by your construction. To make your synthetic data slightly more realistic while retaining most of their features that you wanted we could either increase the standard deviation of the regional noise from 0.1 to 0.3---this change is realistic because the regional variance is always larger than the global mean variance:
(1) n_atlantic=global+rnorm(t,mean=0,sd=0.3)
Or we could retain the same combined standard deviation as your two noise terms in n_atlantic, but from a different draw of the random variable than the random variable in global:
(2) n_atlantic=human+nature+rnorm(t,mean=0,sd=sqrt(0.2^2+0.1^2))
For both cases we repeated your MLR and found that the true anthropogenic warming of 0.17 C per decade is correctly estimated to lie within the 95% CI at least 93% of the time for case (1) and at least 94% of the time for case (2). This conclusion is obtained by 10,000 Monte Carlo simulations.
The reason I said above that your example is almost trivial is that except for the small regional noise, n_atlantic is the same as global. The AMO index that you defined is n_atlantic minus its linear trend. So global minus n_atlantic is deterministic (when that small regional noise is absent) and is equal to the linear trend. You do not need MLR to show that when your AMO is regressed away what is left is the linear trend 100% of the time.
You can also make your example less deterministic and hence less trivial, by smoothing your AMO index as we did in our paper. Even with everything else remaining the same as in your post 117, you would find that with this single change in your procedure the true value of the anthropogenic warming rate is found to lie within the 95% CI of the MLR estimate 2/3 of the time.
In our PNAS paper, we said that because of the importance of the results we needed to show consistency of the results obtained by different methods. The other method we used was wavelet. Applying the wavelet method to your example and to all the cases mentioned here we obtain the correct estimate of the true value for anthropogenic warming rate over 98% of the time. The wavelet method does not involve detrending and can handle both linear or nonlinear trends.
For the realistic case considered by us in our papers, the anthropogenic warming rate was found to be approximately 0.08+/-0.02 C per decade by the two methods, which gives us confidence that our result was not affected by a particular method. The smaller error bars (compared to your unrealistic example) bound the true value far below the value of 0.17 C per decade of Foster and Rahmstorf (2011).
In reply to post 123 by Dikran Marsupial:
It appears that your entire case hinges on a misidentified word.
"The regression coefficient for AMOd is 2.7685 +/- 1.2491, note that this interval DOES NOT contain the true value, which is zero."
How do you know the true value for the AMO is zero? Must it be that in your mind you identified the 70-year oscillation as the AMO? But by construction your AMOd regressor does not contain any 70-year signal, nor does your observation. In fact there does not exist any 70-year signal anywhere in your example. So it trivially follows that you will not get any 70-year signal by multiple regression. It now becomes a word game on what you call your AMOd. You could just as well call it the "quadratic". Then you always get zero for the nonexistent 70-year AMO cycle in your MLR.
It is also easy to understand why your MLR yields a linear trend when the anthro component in your synthetic observation consists a linear plus a quadratic trend. Let's for a moment ignore the 150-year natural cycle; it does not affect the argument that I am making. Then your AMOd is just the anthro trend minus the linear trend, which is just the quadratic term. When you do the MLR with AMOd being the quadratic regressor, and you use a linear trend for your anthro regressor, observation then gets divided into a quadratic term that goes into AMOd and a linear term that goes into anthro. There is no secular trend left in the residual. The final adjusted anthro trend is the same as the regressed linear trend.
To put it in a different way, without the 150-year natural cycle (which is a red herring in your example), observation=linear+quadratic+noise. The two regressors you have now could have been called linear and quadratic. After one round of MLR, the two regressors plus noise give a good model of your original observation. Now let's rename linear the anthro regressor, and quadratic the AMOd regressor, and conclude: the MLR gives an erroneous linear trend when the true value is linear plus quadratic, and the true value of the AMO, which is zero for the entirely missing 70-year cycle, is not included in the 95% confidence interval of regression coefficient of AMOd.
There is no contradiction between the MLR result and their true values in your example. The contradiction arises only when you give them wrong names.
Prof. Tung wrote: "How do you know the true value for the AMO is zero?"
I know this by construction. The point of the thought experiment was to demonstrate that there are hypothetical sitiuations where the regression model used in your paper underestimates the effect of anthropogenic emissions on observed temperatures and missattributes this warming to AMO.
Forgetting for the moment whether the scenario in the thought experiment is plausible or not, do you agree that the thought experiment does show that there can be circumstances where the regression analysis can fail and missattribute warming due to anthropogenic emissions to the AMO? Yes, or No.
In reply to Dikran Marsupial's post 126: I am not sure if you understood what I was trying to say in my post 125. Of course when there is no AMO in your data you are not going to find an AMO using the method of multiple linear regression analysis (MLR). So the answer is No, not because of the fault of the method, but because you should not have used that method.
On the anthropogenic trend, the way you applied the MLR is to break up the nonlinear anthropogenic trend into a linear part and a quadratic part, using the two regressors, which were called by me in post 125 as linear and quadratic. If you ask the questionh, does the regression coefficient of quadratic in the MLR include the true value of the quadratic term in your anthropogenic trend, the answer is yes. And if you ask the question, does the regression coefficient of linear in the MLR include the true value of the linear part in your anthropogenic trend, the answer is also yes. So the MLR gives you the right answers. But what you were doing is to rename linear anthropogenic, and ask the question, does the regression coefficient of this newly named anthropogenic response include the true value of the anthropogenic response in the observation that you constructed, the answer is not necessarily, depending on how large your quadratic term is.
Please don't get me wrong. I am not here to defend MLR as a fail-proof method. It can fail, and we need to always on guard for that happening. But in this case it "fails" only because you gave your regressors wrong names.
Clarification to my post 127: There are so many parts to the yes or no question that you posed that my single "No" answer may not fully answer the question:
Forgetting for the moment whether the scenario in the thought experiment is plausible or not, do you agree that the thought experiment does show that there can be circumstances where the regression analysis can fail and missattribute warming due to anthropogenic emissions to the AMO? Yes, or No.
The answer is "No" to the first part of the answer: "do you agree that the thought experiment does show". The thought experiment is trivial and inappropriate as I explained later. The answer is "yes" to the second part of the question "do you agree there are circumstances where the regression analysis can fail".
KK Tung wrote "Of course when there is no AMO in your data you are not going to find an AMO using the method of multiple linear regression analysis (MLR)."
You clearly still do not understand the point of the thought experiment. In the thought experiment there is no AMO influence on observed temperatures, but your MLR procedure DOES find one, even though it doesn't exist. That is the problem.
In reply to post 129 by Dikran Marsupial: I thought I was quite clear already, but it seems that I needed a lesson in communication, or I was trying to be too polite, which hinders communication in forums like this. When I said:
"How do you know the true value for the AMO is zero? Must it be that in your mind you identified the 70-year oscillation as the AMO?''
I meant it as a rhetorical question. The answer of course is that you did not put it in your example. It was entirely in your head, and you did not tell your MLR what you meant by AMO. When you replied :"I know this by construction.". You seemed to miss the irony.
I thought I had explained it:
"But by construction your AMOd regressor does not contain any 70-year signal, nor does your observation. In fact there does not exist any 70-year signal anywhere in your example. So it trivially follows that you will not get any 70-year signal by multiple regression. It now becomes a word game on what you call your AMOd. You could just as well call it the "quadratic". Then you always get zero for the nonexistent 70-year AMO cycle in your MLR."
Now in post 129, you continue to miss the point that I was trying to make, but now you think I was missing your point:
"You clearly still do not understand the point of the thought experiment. In the thought experiment there is no AMO influence on observed temperatures, but your MLR procedure DOES find one, even though it doesn't exist. That is the problem."
"My procedure" found something, but it was not an AMO. The fact that you gave it the name AMOd does not make it an AMO. Please do your thought experiment again but this time give your AMOd the new name quadratic.
KK Tung, wrote "My procedure" found something, but it was not an AMO. The fact that you gave it the name AMOd does not make it an AMO."
Similarly a variable in your MLR analysis is labelled as being AMO but that doesn't mean that it actually is the true AMO signal. As I have pointed out linear detrending does not remove all of the anthropogenic contamination of the AMO signal, nor for that matter does it remove the contamination due to other natural forcings, such as solar and volcanoes. It is this contamination by both natural and anthropogenic forcings that means that some of the warming due to anthropogenic forcing can be misattributed by your MLR analysis to the variable that you have labelled as AMO.
Dr. Tung - I believe that what Dikran has shown with his synthetic data case is that inappropriately detrending (linearly in his synthetic experiment) cyclic forcings, forcings superimposed on nonlinear trending anthropogenic forcings, causes a clear mixing of the signals. And his synthetic data shows a corresponding reduction in attribution to any nonlinear components, errors in identifying known inputs.
I would also agree with his last comment about correct component labeling.
By extension the same method of analysis (MLR), applied in your paper, is subject to the same issues - that a linear detrending of a cyclic signal (AMO) that is potentially a superimposition on a nonlinear trend (anthropogenic and other forcings, known to be nonlinear in sum) can and will lead to false conclusions about anthropogenic attribution.
A simple linearly detrended AMO by definition suffers from an undetermined amount of multicollinearity with nonlinear forcings. Separate methods for identifying the shape of the underlying trends, upon which the AMO is superimposed, must be used to avoid this problem.
In reply to post 131 and post 132: Of the three examples, two by Dikran and one by Dumb Scientist, the example by Dumb Scientist is logically the most correct. His nature contains what in his mind is the 70-year AMO signal, and that such a signal is present in both his global mean data and his N. Atlantic data. The latter was used to define his AMO index after linearly detrending the n_atlantic data. There is no disconnect between what he thinks in his own mind of what an AMO signal is and what he tells his MLR. In contrast, in Dikran's revised example, the one we are currently debating, his natural has 150 year period. Whether it is 150 year or 70 year period does not matter in this hypothetical example, but it matters what he thinks in his mind is the AMO, especially if he does not tell his MLR what he thinks. In his mind he thinks that the AMO should have a 70 year period, but there is no 70-year period oscillation in his global data nor in his AMO index. His AMO index is simply anthro plus this 150 year natural oscillation, later detrended. In addition, and this fact is important, he has both natural and AMOd as his regressors. In contrast, Dumb Scientist only has one of these two. In Dikran's case, the 150-year oscillation belongs to natural. His AMOd is empty as far as oscillation is concerned. What it contains is mostly anthro linearly detrended, and so it contains mostly a quadratic anthro term. That was why I suggested that his AMOd should be renamed quadratic.
Let's redo his thought experiment after the renaming: The regressors are quadratic, natural and linear. There are no AMO regressor because it is not in the global data, and, in his mind Dikran does not think his 150 year oscillation in natural is an AMO. After the MLR is performed, do we get the right answer? There is no AMO index in the regression and therefore the MLR will not give you any amplitude for the AMO, which has 70-year period and no amplitude in the synthetic data. So there is no contradiction here. His natural regressor yields his 150 year oscillation and thus also gets him the right answer. His quadratic yields the quadratic part of his anthro. His linear yields the linear part of his anthro. The MLR is doing what it is supposed to do.
Now consider the logic of the thought experiment if we now say the quadratic regressor should tell us something about a 70-year oscillation with zero amplitude. In reality quadratic gave us an amplitude for the quadratic term in anthro which is quite large and bounded away from zero. Dikran then concluded that this gives the wrong answer for the AMO. It is wrong, in his mind, because he had given quadratic the name AMOd, and by doing so the MLR should magically know that the AMO should have a 70-year period.
In the observation, the global mean data has a quasi 70-year oscillatory signal. The North Atlantic has a similar 70-year signal. It is the North Atlantic data that is being used to define what we called the AMO. How you detrend it is subject to debate, but the logic of Dumb Scientist's example is clear, when he used the n_atlantic data to define the AMO index, but the logic of Dikran's example is not.
KK Tung@133 O.K. for the moment lets forget about AMO and concentrate on the technical limitation of MLR that is central to the point being made.
Say we have a variable of interest, Y, and three possible causes, A, B and C, which we have observed over 150 uints of time, T. It so happens that signal A rises quadratically with T:
A = 0.00002*(T + T.^2);
Signal B is sinusoidal in nature
B = 0.1*sin(3.7*pi*T/150);
Signal C is formed from an unobserved signal D plus contamination from A and B
D = 0.05*sin(3.7*pi*T/150);
C = D + 0.5*A + 0.5*B;
The signal of interest happens to be a noisy linear combination of A, B and D.
Y = A + B + D + 0.1*randn(size(T));
We can work out the linear rate of increase in Y due to A by linear regression
X = [ones(size(T)), T];
[beta,betaint] = regress(A, X);
ebar = diff(betaint');
ebar = 0.5*ebar(2);
true_A = 10*beta(2);
giving
Now say we suspect that the signal C has been contaminated by signal A, so we try linearly detrending C to remove the contamination, giving detrended signal Cd
X = [ones(size(T)), T];
beta = regress(C, X);
Cd = C - beta(2)*T;
which looks like this:
We now perform our regression exercise to attribute changes in Y to A, B and Cd, however, rather than using A directly, a simple linear trend is used as a proxy.
X = [ones(size(T)) B-mean(B) Cd-mean(Cd) T-mean(T)];
[beta,beta_ci,residual] = regress(Y, X);
model = X*beta;
Giving a reasonably good fit:
Looking at the confidence intervals for the regression coefficients, we see that
signal B: [0.0248 0.7946]
signal Cd: [0.6460 1.7664]
linear trend: [0.0013 0.0025]
note that the confidence interval for the linear trend, which is being used as a proxy for signal A, does not include the true value of the linear trend in Y due to A, which is 0.003.
Again, we combine the linear trend with the residual to determine the deduced linear trend due to A
deduced_A = X(:,4)*beta(4) + residual;
X = [ones(size(T)), T];
[beta,betaint] = regress(deduced_A, X);
ebar = diff(betaint');
ebar = 0.5*ebar(2);
true_A = beta(2);
and get this result
Note that the confidence interval for the linear trend in Y due to signal A does not include the true value (0.003).
Prof. Tung, in this synthetic example, do you agree that the MLR regression method significantly underestimates the effect of signal A on signal Y?
The question-answer-question sequence on this thread appears in danger of hitting resonance so I wonder if reforming the question would help.
T&Zh13 and KK Tung's first SkS post on this subject has argue coherently that an Anthopogenic Regressor of non-linear form does not impact greatly the results when included in the MLR analysis.
In this thread, it has been demonstrated by Dikran Marsupial & also Dumb Scientist that the MLR analysis is sensitive to an underlying quadratic trend if a sinusoidal signal used in the MLR is linearly detrended when the trend it contains is quadratic.
In the first SkS post KK Tung describes how the best fit for an Anthropogenic Regressor is quadratic in form.
Given this situation, here is the question:-
Why is the AMO used in this MLR analysis still detrended linearly?
Perhaps those who are discussing these issues should read THIS paper before continuing further:
http://link.springer.com/content/pdf/10.1007%2Fs00382-013-1669-0.pdf
In reply to MA Rodger at post 135: Four of us, Dikran Marsupial, Dumb Scientist, Jiansong Zhou and I, have spent hours making tens of thousands of Monte Carlo simulations trying to answer the question: if the anthropogenic signal is highly nonlinear (quadratic or fifth order polynomial), will the linear detrending of the AMO index used in MLR necessarily leave us with a wrong linear anthropogenic trend? The correct summary of our efforts so far ( I have not gotten to post 134 yet, but will shortly) should be, in my humble opinion, that we have not found such an example (although we should always be on guard for such a possibility). This is despite some of the extreme examples constructed and discussed here, and undoubtedly more such examples have been tried but not shown here ( I know we have tried many). A thank you is in order to the three of you.
I therefore disagree with your summary:
In this thread, it has been demonstrated by Dikran Marsupial & also Dumb Scientist that the MLR analysis is sensitive to an underlying quadratic trend if a sinusoidal signal used in the MLR is linearly detrended when the trend it contains is quadratic.
In all logical and semi-realistic cases, the MLR so far has yielded the right answer within its 95% confidence internal, although in some cases, the "right" answer is useless because the error bars are too large. We think we understand why in some of these hypothetical cases the error bars are so large. Fortunately the error bars are usefully smaller for the real data.
Given this situation, here is the question:-
Why is the AMO used in this MLR analysis still detrended linearly?
Please suggest a better way if you know of any. Note that to minimize collinearity in the MLR, the AMO index preferrably should not contain a trend, but you are encouraged to suggest different ways for detrending.
Dr. Tung
I would strongly suggest theTrenberth Shea 2006 methodology, supported by Anderson et al 2012, as one detrending methodology worth considering.
At the very least, I would suggest repeating your analysis with these and/or with a simple quadratic detrending - and determining the sensitivity of your analysis (and conclusions) to the choice of detrending method. That issue is, I believe, the core of these discussions, and a question well worth answering.
"KR I would strongly suggest theTrenberth Shea 2006 methodology, supported by Anderson et al 2012, as one detrending methodology worth considering."
KR,
I disagree. All these ad-hoc methods of calculating the AMO are not rationalized and if you read the article I listed before you will see that these variants of the AMO ALL struggle when it comes to deciphering the proper signal. Personally I use two versions and compare the results of each. One is the detrended first component of North Atlantic SSTs and the other is the Van Oldenborgh et al, 2009. They're both wrong but I believe that reality lies between the two. Once again reading that previous study I linked to here:
http://link.springer.com/content/pdf/10.1007%2Fs00382-013-1669-0.pdf
Should be read by everyone while discussing this issue.
robert way - While there are many ways to calculate the AMO, I would disagree about Anderson et al 2012 being ad hoc; they are using PCA to estimate the anthro versus natural variation components; they have numeric support for their position. And they agree with the Trenberth and Shea 2006 method.
Regardless - Any comparison of Dr. Tungs technique against different AMO estimations would provide a sensitivity analysis for those variations in AMO definition. Dr. Tung has not performed such a check - and until/unless he does, I do not feel his conclusions stand given the various counterexamples of colinearity contamination discussed on these threads.
KR testing the sensitivity of the analysis to the choice of AMO definition would indeed be a good thing, however they would all be susceptible to the problem of contamination with anthropogenic and natural forcings, and hence the resulting attribution will still be at best questionable.
Dr. Tung - My apologies, I linked to entirely the wrong paper in this comment: I meant to refer to the Ting et al 2009 discussion on PCA separation of internal variability and anthropogenic contributions.
In reply to KR at post 140 and 142: I did report the result of MLR using Trenberth and Shea's AMO index. The 50-year anthropogenic trend is 0.1 C per decade. There was a problem with collinearity because that index has a negative trend, and I discussed why it has such a negative trend. I will try to put these sensitivity calculations together, along with a discussion of Ting et al 2009 paper, in a separate post.
I had replied to your question on the Anderson et al paper. As far as I am concerned that issue was settled.
In reply to Robert Way at post 139: I agree with you. Not knowing what the true AMO is, all these definitions of the AMO index are ad hoc. Enfield's definition of the AMO index involves linear detrending of the N. Atlantic sea surface temperature (SST). Many on this thread worried that some nonlinear part of the trend may still remain in the AMO index thus defined. Many felt strongly that the Trenberth and Shea definition of the AMO index should be used. This index is the N. Atlantic mean SST minus the global mean SST. The assumption of those who thought this definition is more appropriate is that this way the nonlinear anthropogenic trend can be removed. I discussed this issue in part 2 of my post: The N. Atlantic mean SST trend is smaller than the global SST trend, and so this subtraction takes out too much. So right there we know there is an error. Technically the presence of a trend in the regression index also creates a problem of collinearity. An approach that we have taken is to use different methods and hope that the results are consistent. The wavelet method may have its own problems, but these problems are orthogonal to the problem of the MLR as no detrending is involved. Alternatively, we could do the MLR using different definitions of the AMO index. As Robert Way put it, we know that there could be some possible defect with any ad hoc definition we can come up with, but hopefully the true answer may lie in between. Even better if the error bars are small. I will give you a summary of this sensitivity calculation soon.
KK Tung @144 says:
I would be fascinated to hear how, a priori, KK Tung knows that absent any change of forcing over the twentieth century the North Atlantic SST would have had a neutral or positive trend. Absent that a priori knowledge, he cannot know that subtracting global SST from North Atlantic SST to determine the AMO is a mistake, or at least not on the grounds he states (ie, the difference in trends). KK Tung may think the absence of forcing guaranttees the absense of trend; but given an unforced oscillation in SST, a trend can be produced by differences in phase over the period of the trend. More importantly, as the AMO is avowedly irregular both as to period and amplituded, such irregularity can produce a trend even the period of the trend is in phase. It appears to me, therefore, that his claimed "error" amounts to no more than a circular appeal to the Enfield's definition, which gives him his "knowledge" of the phase, period and amplitude on which basis he dismisses the Trenberth definition.
Turning to the Enfield definition, the one thing we do know for sure about the AMO is that the Enfield definition is ad hoc. Specifically, different defined lengths over which the linear trend is taken will generate different strengths of the AMO at different times. If we take the period 1880-2010 ad defining the linear trend, for example, all periods prior to 1850 will have a strong positive AMO phase. Because it is ad hoc, we know the Enfield definition is in error. It may, however, be useful over a limited period. That it is more usefull than the Trenberth definition over any period, however, is something that is yet to be shown.
KK Tung wrote "Many on this thread worried that some nonlinear part of the trend may still remain in the AMO index thus defined."
Not "may" but "will"; this is self-evident, linear detrending cannot possibly remove a non-linear component of the trend as it is a linear method. Over a short period, a linear trend may be a reasonable approximation to the sum of all anthropogenic and natural forcings (c.f. Taylor series expansion), but on the scale of a century this is clearly not a reasonable assumption.
Do you accept that the AMO signal will remain contaminated by any non-linear component of the forcing? If "no", please explain how linear detrending can completely remove the effects of a non-linear contamination.
KK Tung @137
While the discussion is considering appropriate trends, perhaps it is timely to extend the discussion to the identified trend that T&Zh13 failed to attribute. The Residuals from assuming the QCO2(t) function are shown inset in Figure 3 in Part One of this post where they are described thus:- "Except for s a minor negative trend in the last decade in the Residual, it is almost just noise."
I had wondered if this "minor negative trend" was the " the recent slowing of the (global) warming rates." In T&Zh13 this "slowing" is described as being "included" the "superimposed AMO-related ups and downs," yet the trend within the Residuals suggested to me that perhaps not all this "slowing" had actually been "included." Certainly AMO as per Enfield shows no "slowing" relative to HadCRUT4 that would compensate for the QCO2(t) function (ie the proposed anthropogenic warming contirbution) and this fuelled my curiosity, and prompted my question on this @112 above.
Looking myself at those Residuals, the "minor negative trend" extends back further than "the last decade," indeed extending back beyond two decades. And is it "minor"when it has a trend of something like 0.6ºC/century? If such a level of trend were added to the trend in the QCO2(t) function, present-day attributable anthropogenic warming would then be running at 1.7ºC/century, pretty much the same answer that Foster and Rahmstorf (2011) arrived at.
So I suggest the "minor negative trend" is not "minor."
I would also add that it is also wrong (strong word) to describe the rest of these Residuals as "almost just noise." Closer examination shows otherwise.
By way of illustration for the comment @147. ( I assume the graph is visible to all.)
The "minor negative trend" actually is the " the recent slowing of the (global) warming rates" which remain entirely unattributed after the MLR analysis. (Contrary to my comment @147, it would of course subtract from the rate of anything it was attributed to.)
And bar minor excurtions, for just over half the record the HadCRUT4 signal survives unattributed at 50% amplitude. Can this be right?
Replying to MA Rodger in posts 147 and 148: You missunderstood the context of that statement about a minor negative trend in the residual. In the method of MLR that we used, the residual is added back to the regressed "anthropogenic" signal in the first round to obtain the "adjusted data" from which then the anthropogenic trend was finally determined. The result from the first step is not considered final if there is a trend in the residual. One should not attribute it in the intermediate step of the procedure to anything until the process is complete.
Question to Dikran Marsupial on post 134: I don't quite understand your thought experiment. What is an "unobserved signal D"? Whatpurpose did you intend it to serve in this thought experiment? Isn't it the same as B? You can combine D with B and get:
C=0.5*A+(0.05+0.05)*sin(3.7*pi*T/150)
So it should simply be
C=0.5*A+B
Y=A+(0.1+0.05)sin(3.7*pi*T/150)+0.1*radn((size(T))
So it should simply be
Y=A+1.5*B+0.1radn((size(T)).
Maybe there was a typo on the sinusoidal function?