The Planetary Greenhouse Engine Revisited
Posted on 15 June 2011 by Chris Colose
It turns out that significant discussion on the blogs came out of my recent “Even Princeton Makes Mistakes” posting, where I raised issues with an article on global warming by Princeton physicist Will Happer which contained a suspicious number of trivial errors, conspiracy theories, and fallacies. A surprisingly disproportionate amount of response was dedicated to a side comment about the greenhouse effect on Venus that I made in passing-by (e.g., here, here, and Bart Verheggen chipped in too). I notice many issues still plaguing the web with regard to the basic physics behind the greenhouse effect, but also misconceptions behind some of the thermodynamics and radiative transfer in climate studies. In particular, many people still think you can get super-hot temperatures on Venus without a greenhouse effect if you maintained a high surface pressure; others still think the greenhouse effect does not exist because its warming influence in some way violates thermodynamics. Another that I really don't understand is that the lapse rate (the temperature change with height) itself causes high surface temperatures. As such, I thought I'd take the opportunity to cover some of the inner workings behind the greenhouse effect while addressing these points. This may be a bit lengthy, but hopefully educational and a useful reference for future discussions that may arise.
The Greenhouse Effect and Thermodynamics
When we think about problems in planetary climate-- whether it be the greenhouse effect of Venus, Snowball Earth, extreme orbits, the range of habitability around others stars, or what exotic atmospheres one might encounter on other planets-- we must be prepared to think well outside the "climate box" in terms of scenarios and possibilities. Whatever alien situation we can think of however, we are necessarily constrained by the laws of physics to create a self-consistent picture that distinguishes reality from science fiction. Among these laws of physics are the many well-established rules governing the behavior of radiant energy and its interaction with air, and also the statistical behavior of gases in local thermodynamic equilibrium. Just as an incredibly trivial equation of state emerges in the thermodynamic limit from very complex molecular dynamics (which ultimately describes a relationship between fundamental variables in our atmosphere), we can make many general remarks concerning the energy balance and temperature structure of planetary atmospheres, even with exceedingly complex behavior at the interface of fluid dynamics, chemical interactions, and energy/momentum transfer.
The nearby rocky planets (e.g. Mercury, Venus, Earth, Mars) gain and lose energy radiatively, and come into thermal equilibrium when the magnitude of the absorbed solar radiation equals the outgoing emission by the planet (which is in the far-infrared part of the electromagnetic spectrum for all planets in our solar system, but could just as well be primarily in the visible for very hot planets orbiting close to their host star). This is not always the case: on the gaseous planets, observations show that the outgoing thermal radiation exceeds the incoming solar energy by significant amounts (this excess is nearly a factor of three for Neptune). This is because the giant planets have an internal heat source. On Earth or Venus, internal heating takes the form of radioactive decay, although it is negligible for energy budget purposes, since the energy flux is many orders of magnitude smaller than the incoming solar energy flux. Radioactive decay is not responsible for the infrared excess on gas planets either; instead, the interior heat source takes the form of Kelvin-Helmholtz contraction—a way of converting potential energy into kinetic energy as the whole atmosphere contracts into the center (i.e., becoming more centrally condensed), heating the gas interiors. This is a critical component of giant gas planet evolution, and the process is also what makes young stars hot enough in the center to eventually fuse hydrogen, although Jupiter is not nearly massive enough to reach this point.
Introducing an infrared absorbing atmosphere into the picture complicates things, since now radiation is lost to space less efficiently than with no atmosphere (for a given temperature). In essence, the surface temperature acts as a slave to the way energy flows operate between our sun , the planet, and the overlying air and eventually adjusts to maintain equilibrium at the top and bottom of the atmosphere. The critical ingredient for the greenhouse effect (aside from IR absorbers, obviously) is that the temperature structure of the atmosphere is one that declines with height. This is because in order to make the planet lose radiant heat less efficiently, you need to replace the “radiating surface” near the ground with a weaker “radiating surface” in the upper, colder atmosphere (Fig 1)
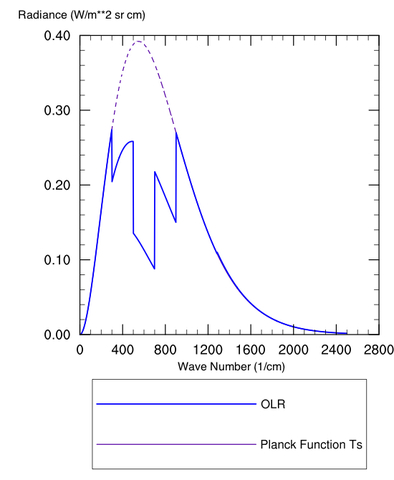
Figure 1: Spectrum (Radiance vs. wavenumber) for a Planck Body at 300 K (purple dashed) and the OLR with an IR absorbing greenhouse gas
Figure 1 is plotted as a somewhat “contrived” greenhouse substance that works like this: Our ground has a temperature Ts, with a colder temperature above the surface (e.g. the stratosphere). Plotted are the Planck function for the surface temperature (purple dashed) and actual outgoing radiation (OLR, curve). The Planck function gives the distribution of energy intensity vs. wavenumber (or wavelength, or frequency, depending on your favorite characterization of an electromagnetic wave) for a blackbody at some specified temperature.
The blue curve titled “OLR” is the actual spectrum of this hypothetical planet with a hypothetical greenhouse gas in the atmosphere. The difference between that blue spectrum and the Planck (purple) spectrum for the ground temperature arises because our greenhouse gas happens to be blocking radiation from exiting directly to space at 600 cm-1 and the surrounding regions. Even toward the “wings” at 400 or 800 cm-1 it is making the atmosphere “partially opaque.” This is fairly standard qualitative behavior for a greenhouse gas, especially CO2, although there are exceptions.
This plot is computed for a fixed temperature, so the end result of adding the greenhouse gas is to reduce the total outgoing radiation (the specific amount is whatever chunk is taken out of the Planck curve). This creates a situation where the planet temporarily takes in more energy than it loses, and as a consequence the ground temperature must rise to increase emission and restore equilibrium.
To think about this another way, emission at wavenumbers where the atmosphere is strongly absorbing will always be closer to a "sensor" that is recording the emission than wavenumbers where the atmosphere is transparent. If the sensor is a satellite looking down from space, it will see warm, surface emission in transparent ("window") wavenumbers, but for opaque wavenumbers, emission emanates from the high atmosphere.
Similarly, for a surface sensor looking up, emission from opaque regions is seen to come from very near the surface, whereas for transparent wavenumbers the sensor is recording the ~3 K temperature of microwave background radiation in space. In this post, we're thinking about the sensor looking down.
Brief Technical aside: Let’s define a “mean radiating pressure" of the planet, which we’ll call pr, where the atmosphere becomes optically thin enough to lose its radiation to space directly rather than being absorbed in a higher layer. Since pressure decreases with height, the radiating pressure will decrease as the optical thickness of the atmosphere increases (i.e., more radiation is preferentially leaking out higher in the atmosphere where it is colder when you add greenhouse gases). Conversely, the radiating pressure is at the surface (pr=ps) with no greenhouse effect. It is easy to show that for an atmosphere whose temperature profile is dry adiabatic, that the radiating pressure is given by:

where the ratio cp/R is approximately 7/2 for Earth air; the numerator in the brackets is the absorbed solar radiation, σ is the Stefan-Boltzmann constant, and Ts is the surface temperature. For Earth, the mean radiating pressure would thus be at ~650 millibars, rather than at sea level (1000 mb) with no atmosphere (in reality, it would be smaller than this, since the real lapse rate is less steep than the dry adiabat). See also Figure 2, to show how decreasing pr increases the surface temperature.
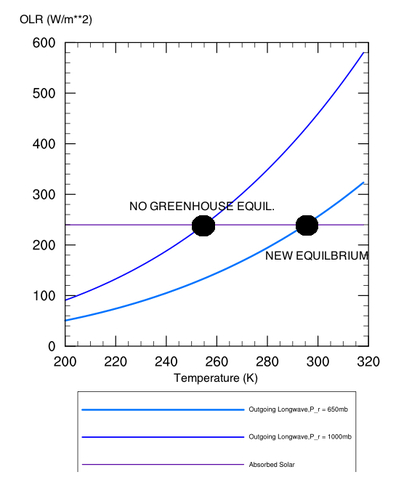
Figure 2: Depiction of how increasing the radiating height of a planet increases the surface temperature. Equilibrium is reached when the outgoing long-wave energy curves intersect the absorbed solar radiation curve.
Does this all violate Thermodynamics?
The reason greenhouse warming does not violate thermodynamics is because the planet is not an energetically closed system, and receives a constant influx of energy from the sun. The reduction in outgoing energy flow by the atmosphere can therefore heat the planet toward a value slightly closer to the solar temperature. If the sun turned off, the greenhouse effect would be irrelevant (even assuming you could keep your atmosphere in the air at all without everything condensing out). Some people on the blogs have claimed that because a colder atmosphere radiates toward a warmer surface, there is some thermodynamic inconsistency with the second law. First, note that I have not said a word about back-radiation to the surface, primarily because it doesn’t give proper insight into the way energy balance is adjusted and determined. But to the point, cold objects still radiate energy and a photon doesn’t care whether it’s traveling toward a warm object. So yes, colder objects can and do radiate toward (and heat!) warmer objects. Standard measurements (from Grant Petty's Radiation book) of back-radiation should be simple proof that this occurs. Keep in mind that the net two-way energy flow is always from warm to cold.
Let’s now compare the theoretical Fig. 1 spectrum with a real Venus spectrum (Fig 3).
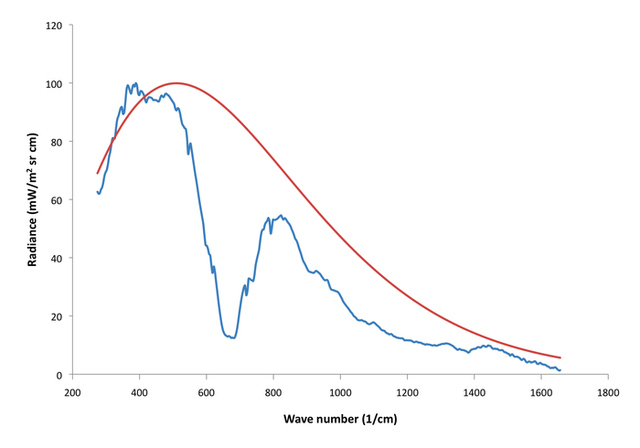
Figure 3:260 K blackbody spectrum (red) with observed Venus spectrum from The Venera 15 orbiter (blue).
Here, the red curve is a 260 K blackbody Planck spectrum and the blue is a typical Venus spectrum I plotted which was obtained from the Soviet Venera 15 orbiter. Keep in mind that the Venusian surface radiates at ~735 K, so the fact that the whole spectrum is seen to radiate at Earth or Mars like temperatures is a good indication that the atmosphere is highly opaque in the infrared spectrum. Most of this is CO2, but other constituents like water vapor, SO2, and sulfur-water clouds are very important too, along with some other minor species.
Some Remarks about Pressure
It has been argued on some blogs that high pressures can cause high temperatures, and the argument has taken a variety of forms. One is that p= ρRT (the ideal gas law) implies that a high p means a high T. Of course, the pressure is 90x higher on Venus but the temperature is only 2-3 times higher than Earth, so such a straightforward proportion obviously doesn’t work. The temperature must satisfy energy balance considerations, so a better way to think about the problem is to fix T (with other information, namely radiation) and solve for the density, which is of course much higher on Venus. You can't get all the information from the equation of state alone. The other argument is that some “insulative” property of gases could keep Venus hot at high pressure, even if the whole atmosphere were transparent to outgoing light. One way to heat Venus would be to compress its atmosphere, but this would be temporary and eventually the temperature must relax back to its equilibrium value determined by energy conservation considerations. The way things work is that heat is sluggishly migrated upward by radiation or convection until it finally reaches a point where the air is optically thin enough to let radiation leak out to space. This doesn’t happen in a transparent atmosphere.
So does pressure matter for the greenhouse effect? The answer is yes, and the prime reason it matters is that collisions between molecules act to “smooth out” absorption and fill in the window regions where air is transparent. Unlike the quantum nature of absorption and emission, the kinetic energy of moving molecules is not quantized, so it is possible for colliding molecules to impart kinetic energy on the absorber and make up the energy deficit required to make a quantum leap from one energy level to another. There are some other broadening mechanisms too, but this is by far most important in the lower atmosphere.
Aside from the fact that a 90 bar atmosphere can hold much more greenhouse gas, pressure broadening is huge on Venus, but you can only smooth things out and fill in the windows so much. Where pressure broadening would really make a difference is to put in a 1 bar atmosphere (even N2) on a very low dense atmosphere like Mars. The reason why Mars does not currently generate a strong greenhouse effect, even at over 90% CO2, is that the spectral lines are too narrow to have a sizable effect. Even with almost two orders of magnitude more CO2 per square meter than Earth, the equivalent width is less on Mars. The equivalent width is a measure of the area of absorption taken out by a molecule (see the wiki article for further explanation on its definition). The following diagrams illustrate the OLR change in a 250 ppm CO2 atmosphere at Earthlike pressure (Fig. 4a) and 100x Earth pressure (Fig. 4b) (note that the same mixing ratio in the 100 bar atmosphere implies more greenhouse gas overall).
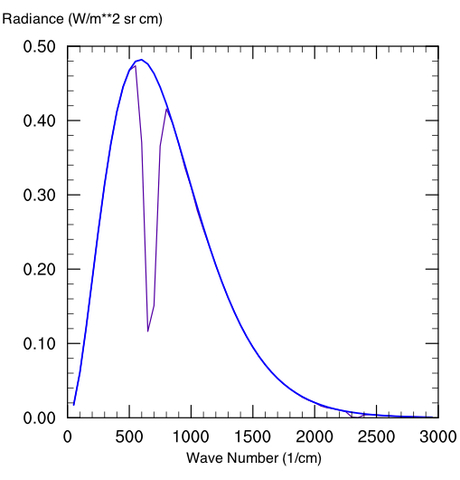

Figure 5: 250 ppm CO2 mixing ratio for an atmosphere at a) Earthlike pressure and b) 100x Earth pressure
Note that at very high CO2 concentrations, a lot of new absorption features come into play that are irrelevant on modern Earth. The water vapor and sulfur-bearing compounds on Venus also help to fill in some window regions considerably. Also unlike Earth, Venus has a non-negligible scattering greenhouse component too (by inhibiting cooling through IR scattering rather than absorption and emission). These make direct planetary comparisons useless, except that Venus is a case in point of how much a greenhouse effect can matter in planetary climate discussions.
Note also that very dense atmospheres also raise the albedo through Rayleigh scattering; this is the same process that make our skies blue. A pure Venusian CO2atmosphere raises the albedo to a moderately high ~40%, somewhat short of its current albedo (~77%, because of clouds), but still higher than Earth. This remark is primarily true for planets orbiting sun-like stars, but for lower temperature stars (like M-dwarfs) the Rayleigh scattering is much less important, since the spectrum of the starlight itself is red-shifted, and Rayleigh scattering favors shorter (bluer) wavelengths.
Could a purely diatomic molecule atmosphere generate a greenhouse effect?
The answer, again, is yes. This may be surprising because something like H2 or N2doesn’t have the molecular symmetry (to make a dipole moment) that we commonly attribute as a defining characteristic of greenhouse gases. Similarly, Pressure broadening doesn’t broaden anything that isn’t there to begin with. But for very dense atmosphere, frequent enough collisions between diatomic molecules can temporarily make a ”four-atom” molecule that behaves like a greenhouse gas. This effect is much more pronounced at colder temperatures, since the time of collision is longer at low velocities. Collision induced (as opposed to broadened) absorption has been best studied on Titan, but it’s important on the gaseous planets, as well as some theoretical atmosphere with several tens of bars of H2 or He that are relatively dense and cold. It’s unimportant on Earth, since the temperatures are high enough and density low enough.
Lapse Rates and Tropopause Height
Several other bloggers have been under the impression that the lapse rate “causes” high surface temperatures on a place like Venus, the idea being that the tropopause is very high and so one can extrapolate down the adiabat very far to reach a high temperature. As should be obvious from the preceding section, the entire reason why you’re allowed to extrapolate such a far distance is because of the greenhouse effect, which increases the altitude where emission in the opaque regions of the spectrum take place. In fact, on Venus the high tropopause is a a consequence of the high optical thickness.
In radiative-convective equilibrium, the atmosphere transports sufficient heat vertically (by convection) to prevent the lapse rate from exceeding some critical value, so that a stratosphere can exist in radiative equilibrium (with a thermal balance between ozone heating and CO2 cooling) atop a troposphere where both radiative and dynamical fluxes are important. The lapse rate just describes the manner in which temperature changes vertically; it isn’t some supply of energy and you need to specify the temperature at the surface by some other means. The reason an adiabatic lapse rate might develop and the height to which it extends is most certainly not independent of radiation, which provides a basis for global energy flows.
An adiabatic lapse rate only needs to develop by convection where air parcels at the surface become buoyant with respect to the air above it. In an infrared transparent atmosphere with no sources and sinks of energy, convection would eventually give out and the tropopause would migrate to the surface, developing a deep isothermal region.
In conclusion, the "greenhouse effect" is a very real physical phenomenon and has no inconsistencies with thermodynamics or any other field of inquiry (and in fact,emerges from these disciplines). It can be just as important in determining the global temperature as the distance to the sun, and is especially important on Venus.
Acknowledgments: I would like to thank Ludmila Zasova for the Venus Venera spectral data used in Figure 3 (which was provided by David Crisp). I also made use of Dr. Ray Pierrehumbert's online Python code that supplements his new textbook for image production.
Further Recommended Reading: Pierrehumbert RT 2011: Infrared radiation and planetary temperature. Physics Today 64, 33-38, online here [PDF]
Greenhouse Effect Revisited, by yours truly
ScienceofDoom - no specific link, as he has a large number of articles on Energy Balance and radiative transfer...great multi-series introduction if you wade through the pages
Comment On "Falsification Of The Atmospheric Co2 Greenhouse Effects Within The Frame Of Physics", by Joshua B. Halpern, Christopher M. Colose, Chris Ho-Stuart, Joel D. Shore, Arthur P. Smith And Jörg Zimmermann, in IJMP(B), Vol 24, Iss 10, Apr 20, 2010, pp 1309-1332
Several part series on Venus, by Brian Angliss, starting with this post































 Arguments
Arguments






























[DB] I took the liberty of breaking your comment up into paragraphs for improved readability.